Suffix Sum of an Array Codes With Visualization
Raj Aryan is passionate about breaking down complex DSA concepts and making coding feel approachable for everyone. With over 500 problems solved on LeetCode, two hackathon wins under his belt, and a 3-star rating on CodeChef, he enjoys helping others level up their programming skills.
Why should you care about suffix sums? They can transform certain operations from linear time to constant time, making your code significantly faster for specific tasks. Whether you're tackling competitive programming challenges, processing large datasets, or optimizing real-world applications, suffix sums provide an elegant solution to many computational problems.
Understanding Suffix Sum
Basic Concept
At its core, a suffix sum is quite simple. For an array A of size n, the suffix sum array S is another array of the same size where each element S[i] represents the sum of all elements from position i to the end of the array.
In other words:
- S[n-1] = A[n-1] (The last element's suffix sum is just itself)
- S[n-2] = A[n-2] + A[n-1] (The second-to-last element's suffix sum includes itself and the last element)
- And so on until S[0] which is the sum of the entire array
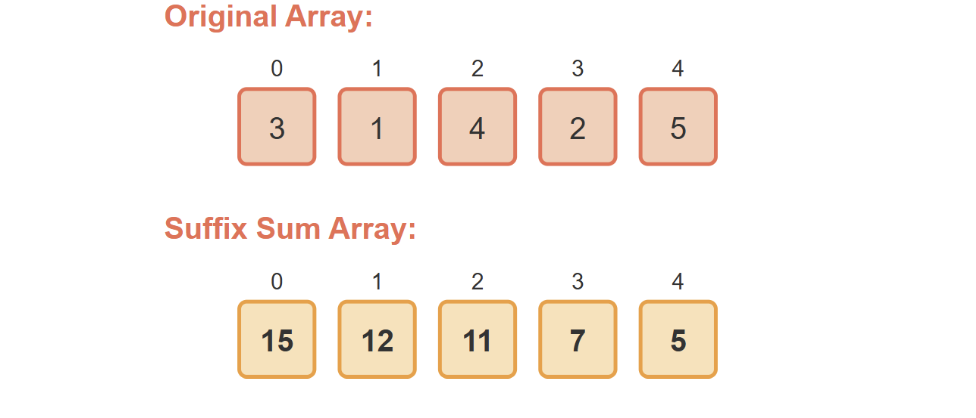
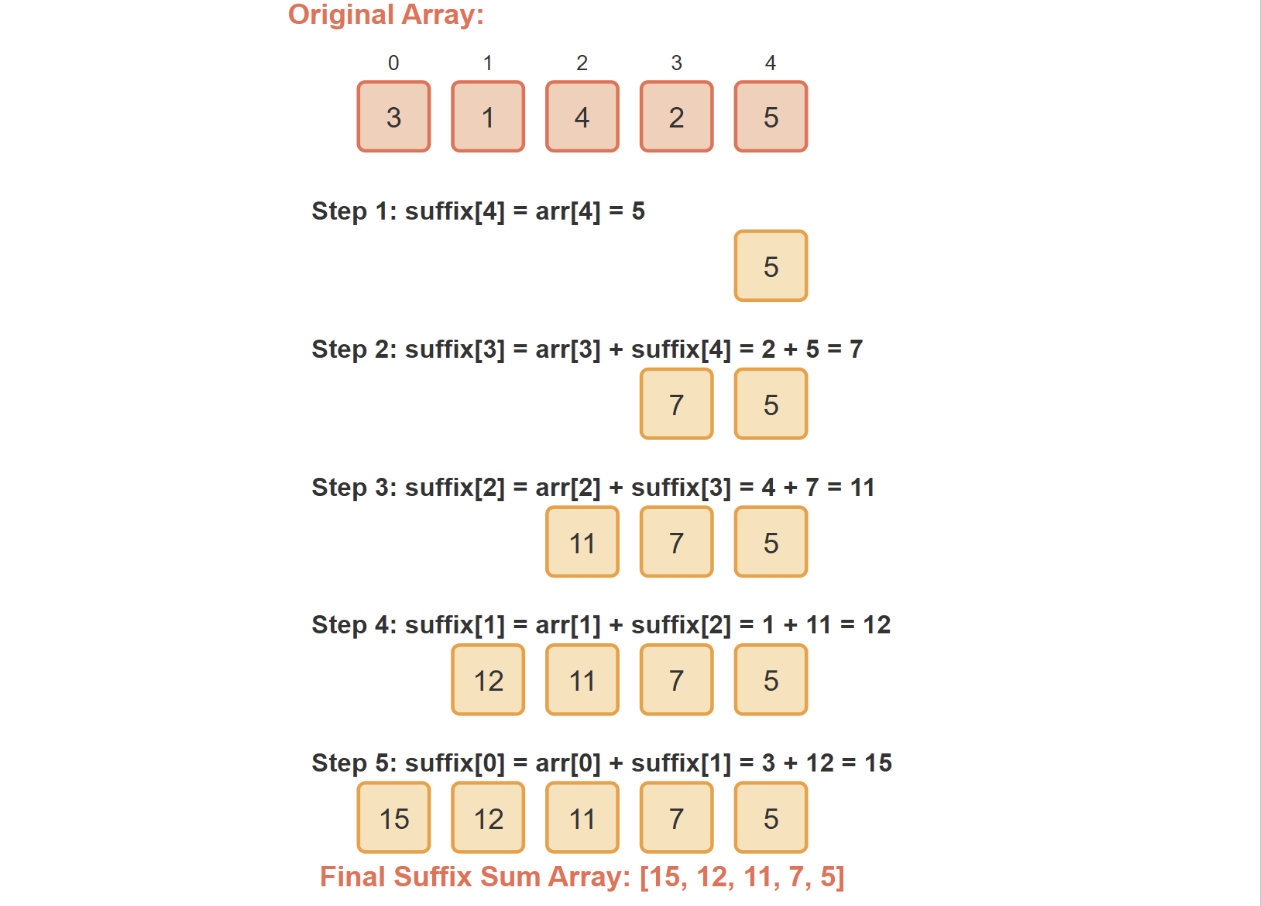
For example, if we have an array [3, 1, 4, 2, 5]:
- The suffix sum array would be [15, 12, 11, 7, 5]
- S[0] = 3 + 1 + 4 + 2 + 5 = 15 (sum of all elements)
- S[1] = 1 + 4 + 2 + 5 = 12 (sum from index 1 to the end)
- S[2] = 4 + 2 + 5 = 11 (sum from index 2 to the end)
Comparison with Prefix Sum
Many programmers are already familiar with prefix sums, which work in the opposite direction:
- Prefix sums start from the beginning and accumulate values moving forward
- Suffix sums start from the end and accumulate values moving backward
Here's a quick comparison:
For array [3, 1, 4, 2, 5]:
- Prefix sum: [3, 4, 8, 10, 15]
- Suffix sum: [15, 12, 11, 7, 5]
Both techniques serve similar purposes but are applied in different scenarios. Sometimes, you might even use both in the same algorithm to solve more complex problems.
Mathematical Definition
Formally, for an array A of size n, the suffix sum array S is defined as:
S[i] = A[i] + A[i+1] + A[i+2] + ... + A[n-1]
Or recursively:
- S[n-1] = A[n-1]
- S[i] = A[i] + S[i+1] for i from n-2 down to 0
This recursive definition leads naturally to efficient implementation approaches.
Code Implementation
Let's implement suffix sums in different programming languages, starting with Python, then moving to C++ and Java.
n = len(arr)
suffix_sum = [0] * n
# The last element's suffix sum is just itself
suffix_sum[n-1] = arr[n-1]
# Fill the suffix sum array from right to left
for i in range(n-2, -1, -1):
suffix_sum[i] = arr[i] + suffix_sum[i+1]
return suffix_sum
# Example usage
arr = [3, 1, 4, 2, 5]
suffix_sums = create_suffix_sum(arr)
print(suffix_sums) # Output: [15, 12, 11, 7, 5]
# Application: Find sum of subarray from index i to j
def query_sum(suffix_sums, arr, i, j):
if j == len(arr) - 1:
return suffix_sums[i]
else:
return suffix_sums[i] - suffix_sums[j+1]
# Example: Sum of elements from index 1 to 3
print(query_sum(suffix_sums, arr, 1, 3)) # Output: 7 (1+4+2)
C++ Implementation
#include <iostream>
#include <vector>
std::vector<int> createSuffixSum(const std::vector<int>& arr) {
int n = arr.size();
std::vector<int> suffixSum(n);
// The last element's suffix sum is just itself
suffixSum[n-1] = arr[n-1];
// Fill the suffix sum array from right to left
for (int i = n-2; i >= 0; i--) {
suffixSum[i] = arr[i] + suffixSum[i+1];
}
return suffixSum;
}
// Application: Find sum of subarray from index i to j
int querySum(const std::vector<int>& suffixSum, const std::vector<int>& arr, int i, int j) {
if (j == arr.size() - 1) {
return suffixSum[i];
} else {
return suffixSum[i] - suffixSum[j+1];
}
}
int main() {
std::vector<int> arr = {3, 1, 4, 2, 5};
std::vector<int> suffixSum = createSuffixSum(arr);
// Print the suffix sum array
std::cout << "Suffix Sum Array: ";
for (int val : suffixSum) {
std::cout << val << " ";
}
std::cout << std::endl;
// Example: Sum of elements from index 1 to 3
std::cout << "Sum of subarray [1,3]: " << querySum(suffixSum, arr, 1, 3) << std::endl;
return 0;
Java Implementation
import java.util.Arrays;
public class SuffixSum {
public static int[] createSuffixSum(int[] arr) {
int n = arr.length;
int[] suffixSum = new int[n];
// The last element's suffix sum is just itself
suffixSum[n-1] = arr[n-1];
// Fill the suffix sum array from right to left
for (int i = n-2; i >= 0; i--) {
suffixSum[i] = arr[i] + suffixSum[i+1];
}
return suffixSum;
}
// Application: Find sum of subarray from index i to j
public static int querySum(int[] suffixSum, int[] arr, int i, int j) {
if (j == arr.length - 1) {
return suffixSum[i];
} else {
return suffixSum[i] - suffixSum[j+1];
}
}
public static void main(String[] args) {
int[] arr = {3, 1, 4, 2, 5};
int[] suffixSum = createSuffixSum(arr);
// Print the suffix sum array
System.out.println("Suffix Sum Array: " + Arrays.toString(suffixSum));
// Example: Sum of elements from index 1 to 3
System.out.println("Sum of subarray [1,3]: " + querySum(suffixSum, arr, 1, 3));
}
}
All three implementations follow the same basic approach:
- Initialize a new array to store the suffix sums
- Set the last element's suffix sum to the last element's value
- Iterate backward through the array, computing each suffix sum as the current element plus the next position's suffix sum
- Include a utility function to demonstrate how suffix sums can be used for range sum queries
Applications
Subarray Sum Queries
One of the most common applications of suffix sums is efficiently answering subarray sum queries. After preprocessing an array to create its suffix sum array, we can find the sum of any subarray in constant time.
For a subarray from index i to index j (inclusive), the sum can be calculated as:
- If j is the last index: suffix_sum[i]
- Otherwise: suffix_sum[i] - suffix_sum[j+1]
This provides an O(1) query time after O(n) preprocessing, which is much more efficient than recalculating the sum each time.
Competitive Programming Problems
Suffix sums are frequently used in competitive programming for problems involving:
- Range queries: Finding sums, products, or other operations over ranges of an array.
- Dynamic problems: Problems where elements are frequently added or removed from the end of an array.
- Cumulative statistics: Tracking running totals, averages, or other aggregate measures.
String Processing
Suffix sums can be applied to strings by converting characters to numerical values. For example:
- Character frequency: Count occurrences of a specific character in any suffix of a string.
- Palindrome checking: Determine if substrings have palindromic properties by comparing character counts.
- Lexicographical ranking: Calculate lexicographical properties of string suffixes.
Array Manipulation
Suffix sums provide efficient solutions for various array manipulation tasks:
- Deletion of marked elements: When removing multiple elements from an array, suffix sums can help maintain the correct structure with minimal shifting.
- Finding equilibrium points: Identifying positions where the sum of elements to the left equals the sum of elements to the right.
- Maximum subarray problems: When combined with other techniques like Kadane's algorithm, suffix sums can help solve maximum subarray problems more efficiently.
Advanced Techniques
Combining with Other Algorithms
Suffix sums become even more powerful when combined with other algorithmic techniques:
- Two Pointers: Using two-pointer techniques with suffix sums can solve sliding window problems efficiently.
def max_average_subarray(arr, k):
n = len(arr)
suffix_sum = create_suffix_sum(arr)
max_avg = float('-inf')
for i in range(n-k+1):
# Calculate sum of subarray using suffix sums
curr_sum = suffix_sum[i] - (suffix_sum[i+k] if i+k < n else 0)
max_avg = max(max_avg, curr_sum / k)
return max_avg
- Binary Search: When searching for a specific sum value within an array, combining suffix sums with binary search can yield logarithmic time solutions.
- Dynamic Programming: Many DP problems benefit from precomputed suffix sums for state transitions.
Optimization Strategies
To make suffix sum implementations even more efficient:
- In-place Calculation: For memory-constrained environments, you can calculate suffix sums in-place by modifying the original array (if permitted).
- Sparse Table: For extremely large arrays where only a few queries are needed, consider using sparse tables to save memory.
- Segment Trees: When both the array and suffix sums need to be updated frequently, segment trees may be more appropriate than simple suffix arrays.
Handling Special Cases
Some scenarios require special attention when working with suffix sums:
- Overflow Prevention: For large arrays or values, be careful about integer overflow. Consider using larger integer types or modular arithmetic.
// Using long long for larger range in C++
std::vector<long long> createSuffixSum(const std::vector<int>& arr) {
int n = arr.size();
std::vector<long long> suffixSum(n);
suffixSum[n-1] = arr[n-1];
for (int i = n-2; i >= 0; i--) {
suffixSum[i] = arr[i] + suffixSum[i+1];
}
return suffixSum;
}
- Empty Arrays: Handle empty arrays gracefully by returning empty suffix sum arrays or appropriate error messages.
- Negative Numbers: When working with problems that involve minimum subarray sums or other optimizations, be careful with the behavior of negative numbers.
Conclusion
Suffix sums represent a fundamental technique in the algorithmic toolkit. By precomputing cumulative sums from the end of an array, they enable constant-time range queries.
The key takeaways from this guide are:
1. Suffix sums precompute the sum of all elements from a given index to the end of an array.
2. They can be created in O(n) time and allow for O(1) range sum queries afterward.
3. They're particularly useful for problems involving range queries, string processing, and array manipulations.
4. When combined with other algorithmic techniques like two pointers, binary search, or dynamic programming, suffix sums become even more powerful.
Consider using suffix sums when your problem involves repeated computation of cumulative values from the end of the array, especially when optimization is important.
For problems requiring bidirectional queries, consider implementing both prefix and suffix sums.
With the foundation provided in this guide, you're now equipped to recognize when suffix sums can provide an elegant and efficient solution to algorithmic challenges.
