Evaluate Reverse Polish Notation: Codes with Visualization
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
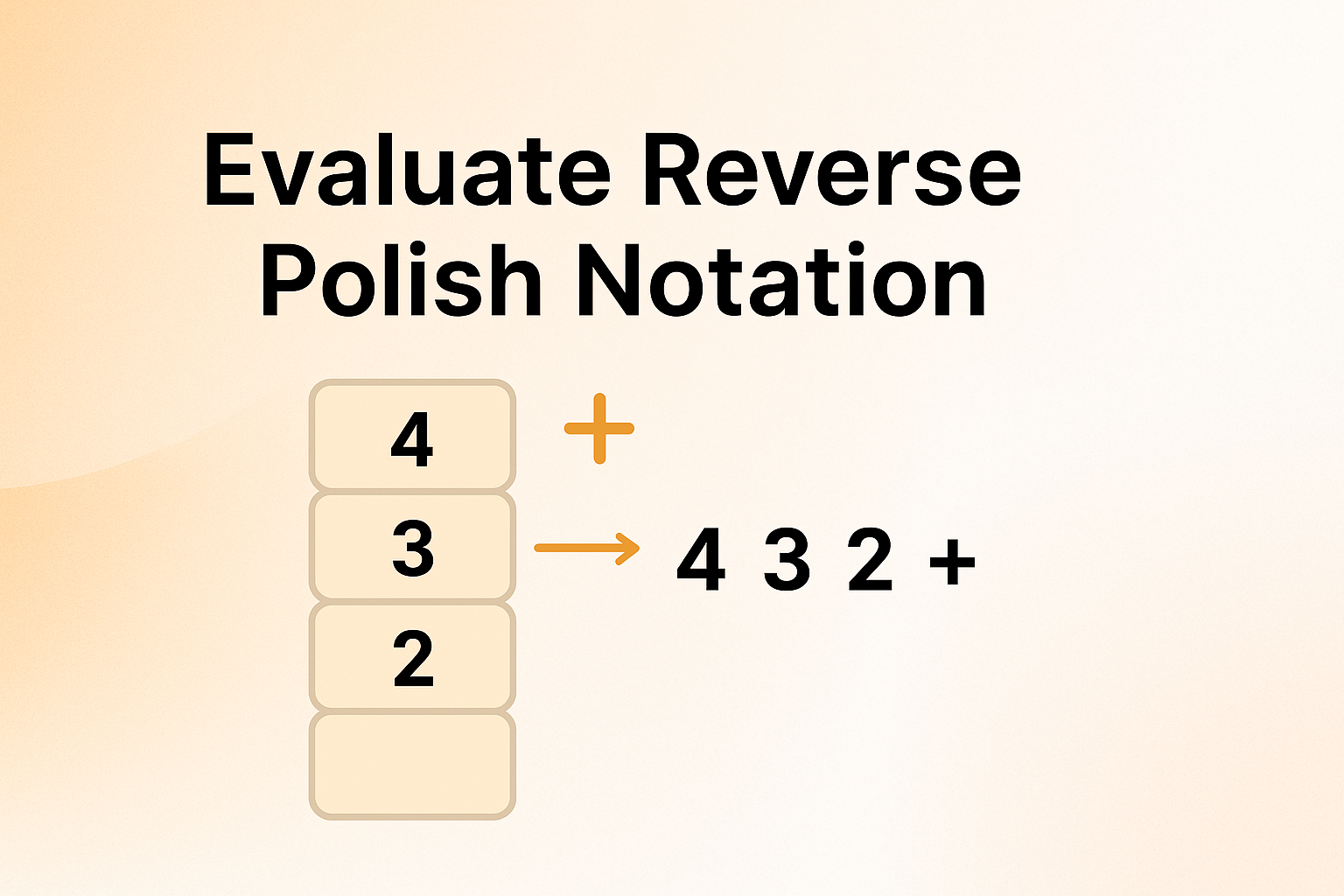
Problem Statement
In Reverse Polish Notation, operators follow their operands. For example, the expression "3 + 4" would be written as "3 4 +". The advantage of this notation is that it eliminates the need for parentheses and operator precedence rules.
You are given an array of strings representing an RPN expression. Each element is either an operator (+, -, *, /) or an integer operand. Your task is to evaluate the expression and return the final value.
For example, if the input is ["2", "1", "+", "3", "*"], which represents (2 + 1) * 3, you should return 9.
Valid operators include +, -, *, and /. Division between two integers should truncate toward zero (integer division).
Brute Force Approach
Explanation
The brute force approach for this problem is actually quite efficient and straightforward. We'll use a stack to keep track of operands and process operators as we encounter them.
- Create an empty stack.
- Iterate through each token in the input array.
- If the token is a number, push it onto the stack.
- If the token is an operator, pop the top two values from the stack, apply the operator, and push the result back onto the stack.
- After processing all tokens, the stack should contain exactly one value, which is the result.
The time complexity is O(n), where n is the number of tokens, as we process each token exactly once. The space complexity is O(n) in the worst case, where most of the tokens are numbers that get pushed onto the stack.
Code(Python)
def evalRPN(tokens):
"""
Evaluates an expression in Reverse Polish Notation.
Args:
tokens: A list of strings representing an RPN expression
Returns:
int: The result of the expression
"""
stack = []
for token in tokens:
if token in ['+', '-', '*', '/']:
# Pop the top two values
b = stack.pop()
a = stack.pop()
# Apply the operator
if token == '+':
stack.append(a + b)
elif token == '-':
stack.append(a - b)
elif token == '*':
stack.append(a * b)
elif token == '/':
# In Python, we need to handle division differently to match the problem's integer division requirement
stack.append(int(a / b)) # This truncates toward zero
else:
# If it's a number, push it to the stack
stack.append(int(token))
# The final result should be the only item left in the stack
return stack[0]Code(C++)
#include <vector>
#include <string>
#include <stack>
class Solution {
public:
int evalRPN(std::vector<std::string>& tokens) {
std::stack<int> stack;
for (const auto& token : tokens) {
if (token == "+" || token == "-" || token == "*" || token == "/") {
// Pop the top two values
int b = stack.top(); stack.pop();
int a = stack.top(); stack.pop();
// Apply the operator
if (token == "+") {
stack.push(a + b);
} else if (token == "-") {
stack.push(a - b);
} else if (token == "*") {
stack.push(a * b);
} else if (token == "/") {
stack.push(a / b); // C++ integer division truncates toward zero
}
} else {
// If it's a number, push it to the stack
stack.push(std::stoi(token));
}
}
// The final result should be the only item left in the stack
return stack.top();
}
};
Code(Java)
import java.util.Stack;
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (String token : tokens) {
if (token.equals("+") || token.equals("-") || token.equals("*") || token.equals("/")) {
// Pop the top two values
int b = stack.pop();
int a = stack.pop();
// Apply the operator
if (token.equals("+")) {
stack.push(a + b);
} else if (token.equals("-")) {
stack.push(a - b);
} else if (token.equals("*")) {
stack.push(a * b);
} else if (token.equals("/")) {
stack.push(a / b); // Java integer division truncates toward zero
}
} else {
// If it's a number, push it to the stack
stack.push(Integer.parseInt(token));
}
}
// The final result should be the only item left in the stack
return stack.peek();
}
}Optimized Approach
Explanation
The brute force approach is already quite efficient for this problem. However, we can make a few optimizations:
- We can use an array instead of a stack data structure for slightly better performance.
- We can use a switch statement (or equivalent) instead of multiple if-else conditions.
- We can avoid repeated string comparisons by checking only the first character of operators.
These optimizations won't change the time complexity, which remains O(n), but they might provide better constant-time performance.
Consider the string = “21+3*”
Step 1: Push 2 onto the stack ,stack = [2]
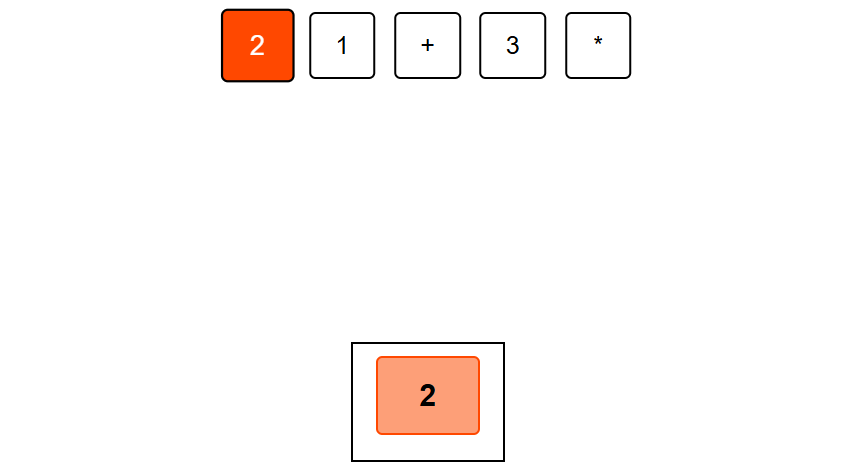
Step 2: Push 1 onto the stack,stack =[2,1]
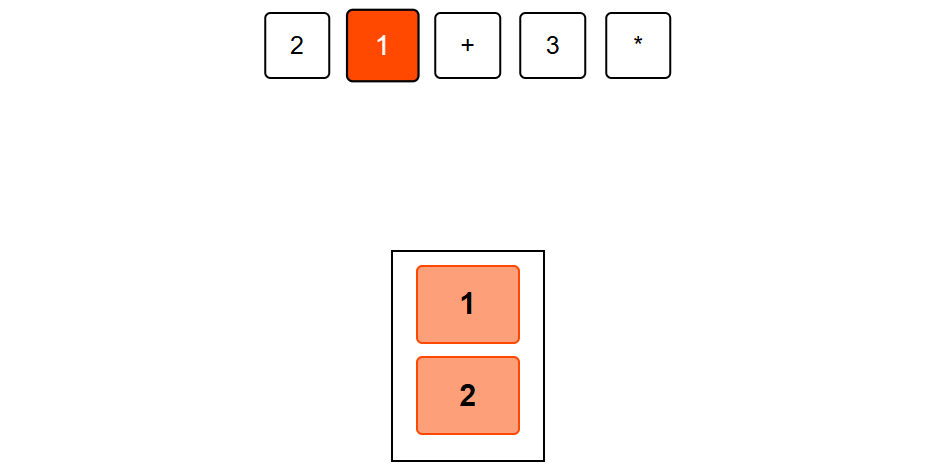
Step 3: Apply + operation. Pop the top two elements (1, 2), add them (2+1=3), and push the result back. Stack = [3]
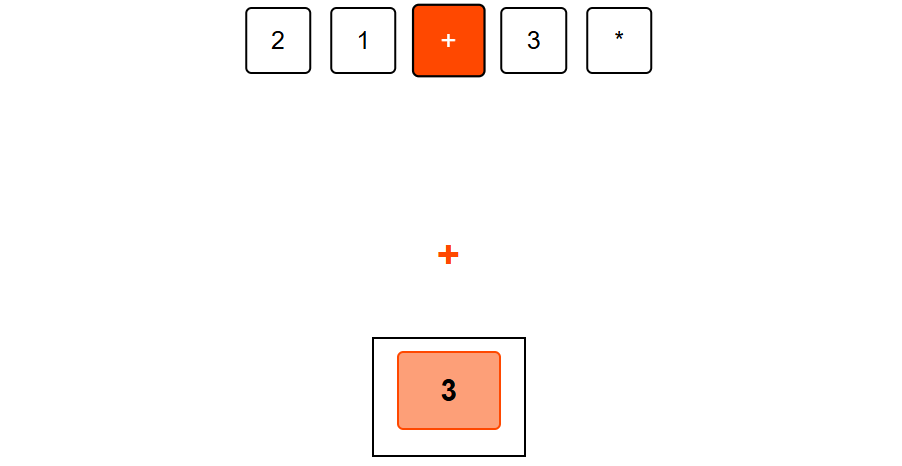
Step 4: Push 3 onto the stack,stack = [3,3]
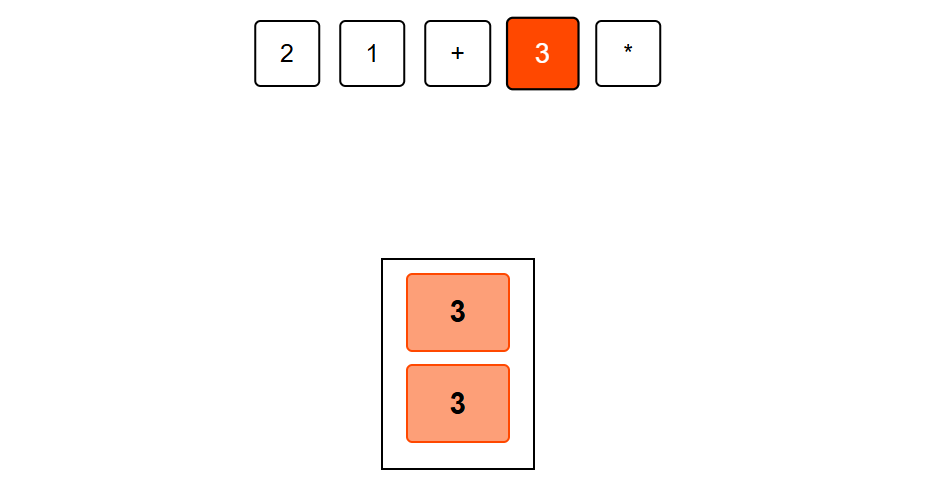
Step 5: Apply * operation. Pop the top two elements (3, 3), multiply them (3*3=9), and push the result back
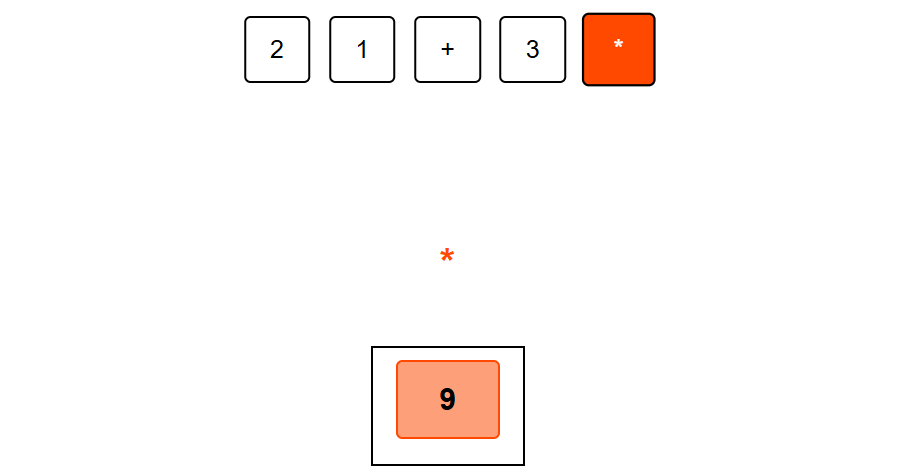
Now the traversal is completed, the element in stack is our answer, in our case its 9.
<visualization-box>
Code(Python)
def evalRPN(tokens):
"""
Evaluates an expression in Reverse Polish Notation (optimized).
Args:
tokens: A list of strings representing an RPN expression
Returns:
int: The result of the expression
"""
# Using a list as a stack for better performance
stack = []
operations = {
'+': lambda a, b: a + b,
'-': lambda a, b: a - b,
'*': lambda a, b: a * b,
'/': lambda a, b: int(a / b) # Truncate toward zero
}
for token in tokens:
if token in operations:
b = stack.pop()
a = stack.pop()
stack.append(operations[token](a, b))
else:
stack.append(int(token))
return stack[0]Code(C++)
#include <vector>
#include <string>
#include <functional>
#include <unordered_map>
class Solution {
public:
int evalRPN(std::vector<std::string>& tokens) {
std::vector<int> stack; // Using vector as a stack for better performance
std::unordered_map<std::string, std::function<int(int, int)>> operations = {
{"+", [](int a, int b) { return a + b; }},
{"-", [](int a, int b) { return a - b; }},
{"*", [](int a, int b) { return a * b; }},
{"/", [](int a, int b) { return a / b; }} // C++ integer division truncates toward zero
};
for (const auto& token : tokens) {
if (operations.find(token) != operations.end()) {
int b = stack.back(); stack.pop_back();
int a = stack.back(); stack.pop_back();
stack.push_back(operations[token](a, b));
} else {
stack.push_back(std::stoi(token));
}
}
return stack.back();
}
};Code(Java)
import java.util.ArrayDeque;
import java.util.Deque;
import java.util.HashMap;
import java.util.Map;
import java.util.function.BiFunction;
class Solution {
public int evalRPN(String[] tokens) {
// Using a Deque as a stack for better performance
Deque<Integer> stack = new ArrayDeque<>();
Map<String, BiFunction<Integer, Integer, Integer>> operations = new HashMap<>();
operations.put("+", (a, b) -> a + b);
operations.put("-", (a, b) -> a - b);
operations.put("*", (a, b) -> a * b);
operations.put("/", (a, b) -> a / b); // Java integer division truncates toward zero
for (String token : tokens) {
if (operations.containsKey(token)) {
int b = stack.pop();
int a = stack.pop();
stack.push(operations.get(token).apply(a, b));
} else {
stack.push(Integer.parseInt(token));
}
}
return stack.peek();
}
}
Conclusion
Evaluating expressions in Reverse Polish Notation is a practical application of stacks. The algorithm is straightforward: process tokens left to right, push operands onto a stack, and when you encounter an operator, apply it to the top two operands.
This problem teaches several important concepts:
1. Stack data structure usage
2. String parsing
3. Operator precedence (which is handled implicitly in RPN)
4. Function mapping to operators
Both our approaches have O(n) time complexity, which is optimal since we need to process each token at least once. The space complexity is also O(n) in the worst case, where most tokens are operands.
What makes this problem valuable is that it demonstrates how the right data structure can simplify a seemingly complex task. By using a stack, we can process expressions without needing to worry about parentheses or operator precedence, showing how clever algorithms can solve problems efficiently.
