Design Stack with O(1) getMin(): Space-Optimized Solution
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
Problem Statement
Design a stack data structure that supports the following operations:
- push(x) – Push element x onto the stack
- pop() – Remove the element on top of the stack
- top() – Get the top element
- getMin() – Retrieve the minimum element in the stack
All operations must have O(1) time complexity, and the solution should use only O(1) extra space (beyond the stack storage itself).
Brute Force Approach
Explanation
The straightforward approach would be to maintain a separate array or list to keep track of minimum values. Each time we push an element, we would compare it with the current minimum and update if needed.
However, this approach uses O(n) extra space, which violates our space constraint. Let's implement it anyway to understand the problem better before moving to the optimized solution.
To understand how this works , lets the following operations,
push(5), push(2), push(4), push(1), push(3)
Initial State:
- stack = []
- min_stack = []
➤ push(5)
- Push 5 onto stack: stack = [5]
- min_stack is empty, so also push 5 onto min_stack: min_stack = [5]
Current Minimum: 5
➤ push(2)
- Push 2 onto stack: stack = [5, 2]
- 2 is less than current min (5), so push 2 onto min_stack: min_stack = [5, 2]
Current Minimum: 2
➤ push(4)
- Push 4 onto stack: stack = [5, 2, 4]
- Since 4 is greater than the current minimum (2), we duplicate the minimum (2) in the min stack. Min_stack = [5 ,2 , 2]
Current Minimum: 2
➤ push(1)
- Push 1 onto stack: stack = [5, 2, 4, 1]
- 1 is less than current min (2), so push 1 onto min_stack: min_stack = [5, 2, 2, 1]
Current Minimum: 1
➤ push(3)
- Push 3 onto stack: stack = [5, 2, 4, 1, 3]
- Since 3 is greater than the current minimum (1), we duplicate the minimum (1) in the min stack.
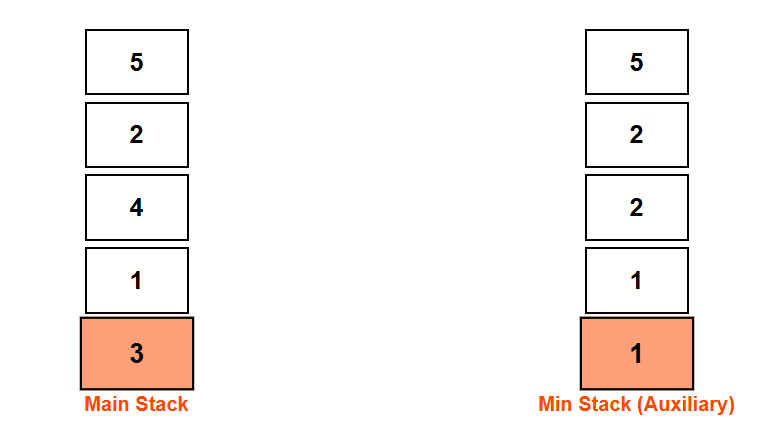
Current Minimum: 1
Code (Python)
class MinStack:
def __init__(self):
self.stack = []
self.min_stack = [] # Extra space to track minimums
def push(self, val: int) -> None:
self.stack.append(val)
# If min_stack is empty or val is smaller than current minimum
if not self.min_stack or val <= self.min_stack[-1]:
self.min_stack.append(val)
def pop(self) -> None:
if not self.stack:
return
# If the element being popped is a minimum, remove from min_stack too
if self.stack[-1] == self.min_stack[-1]:
self.min_stack.pop()
self.stack.pop()
def top(self) -> int:
if self.stack:
return self.stack[-1]
return -1 # Stack is empty
def getMin(self) -> int:
if self.min_stack:
return self.min_stack[-1]
return -1 # Stack is empty
Code (C++)
#include <stack>
#include <climits>
class MinStack {
private:
std::stack<int> stack;
std::stack<int> minStack; // Extra space to track minimums
public:
MinStack() {
// Constructor
}
void push(int val) {
stack.push(val);
// If minStack is empty or val is smaller than current minimum
if (minStack.empty() || val <= minStack.top()) {
minStack.push(val);
}
}
void pop() {
if (stack.empty()) {
return;
}
// If the element being popped is a minimum, remove from minStack too
if (stack.top() == minStack.top()) {
minStack.pop();
}
stack.pop();
}
int top() {
if (stack.empty()) {
return -1; // Stack is empty
}
return stack.top();
}
int getMin() {
if (minStack.empty()) {
return -1; // Stack is empty
}
return minStack.top();
}
};
Code (Java)
import java.util.Stack;
class MinStack {
private Stack<Integer> stack;
private Stack<Integer> minStack; // Extra space to track minimums
public MinStack() {
stack = new Stack<>();
minStack = new Stack<>();
}
public void push(int val) {
stack.push(val);
// If minStack is empty or val is smaller than current minimum
if (minStack.isEmpty() || val <= minStack.peek()) {
minStack.push(val);
}
}
public void pop() {
if (stack.isEmpty()) {
return;
}
// If the element being popped is a minimum, remove from minStack too
if (stack.peek().equals(minStack.peek())) {
minStack.pop();
}
stack.pop();
}
public int top() {
if (stack.isEmpty()) {
return -1; // Stack is empty
}
return stack.peek();
}
public int getMin() {
if (minStack.isEmpty()) {
return -1; // Stack is empty
}
return minStack.peek();
}
}
Optimized Approach
Explanation
To achieve O(1) space complexity, we need to be clever about how we store information. Instead of maintaining a separate stack for minimums, we can encode the minimum information within the main stack itself.
The key insight is to store the difference between the current element and the current minimum. Here's how it works:
- For each element x, we store x - minSoFar
- If this value is negative, it means x is the new minimum
- When retrieving the actual value, we need to decode it based on the current minimum
This approach allows us to track minimums without additional data structures.
Lets consider the following operations:
push(5), push(2), push(4), push(1), push(3), pop(), pop()
Initial State:
- stack = []
- min_val = ∞
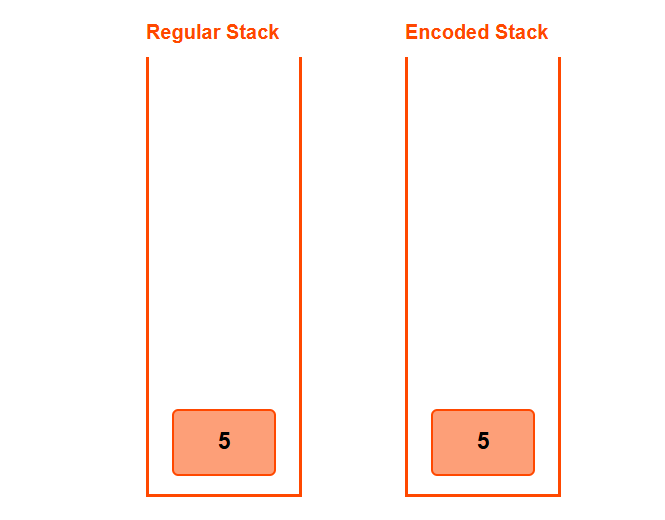
➤ push(5)
- Stack is empty, push 0
- min_val = 5
stack = [0], min_val = 5
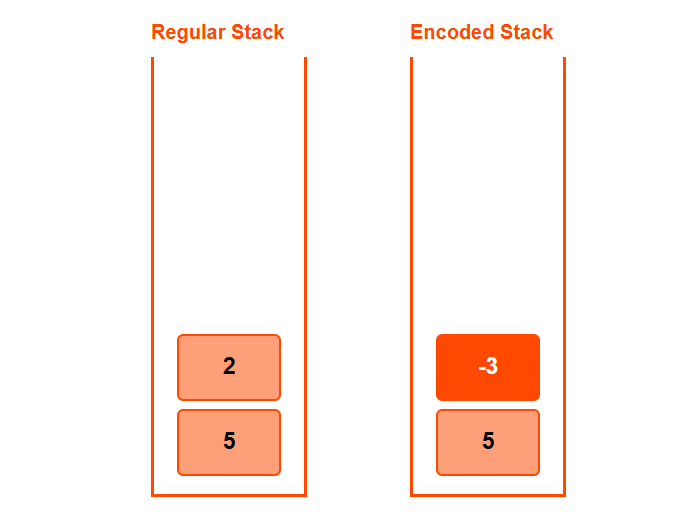
➤ push(2)
- diff = 2 - 5 = -3 (new min)
- Push -3 and update min_val = 2
stack = [0, -3], min_val = 2
➤ push(4)
- diff = 4 - 2 = 2
- Push 2, min remains
stack = [0, -3, 2], min_val = 2
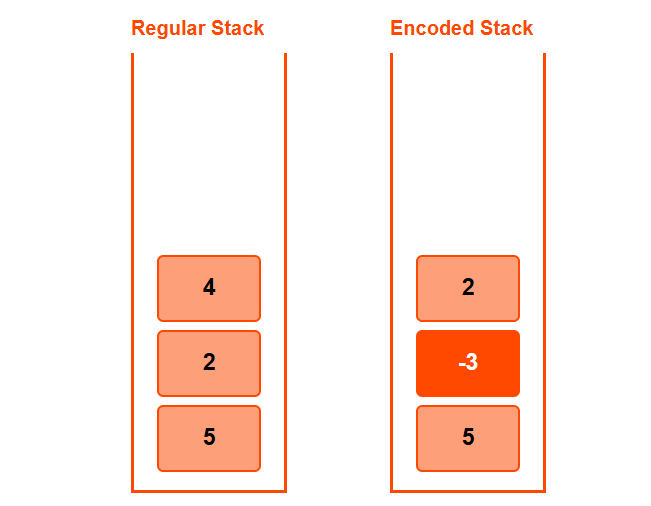
➤ push(1)
- diff = 1 - 2 = -1 (new min)
- Push -1 and update min_val = 1
stack = [0, -3, 2, -1], min_val = 1
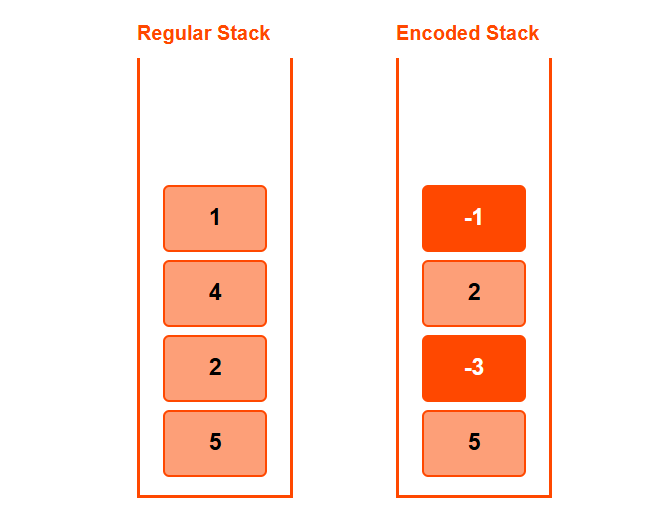
➤ push(3)
- diff = 3 - 1 = 2
- Push 2, min remains
stack = [0, -3, 2, -1, 2], min_val = 1
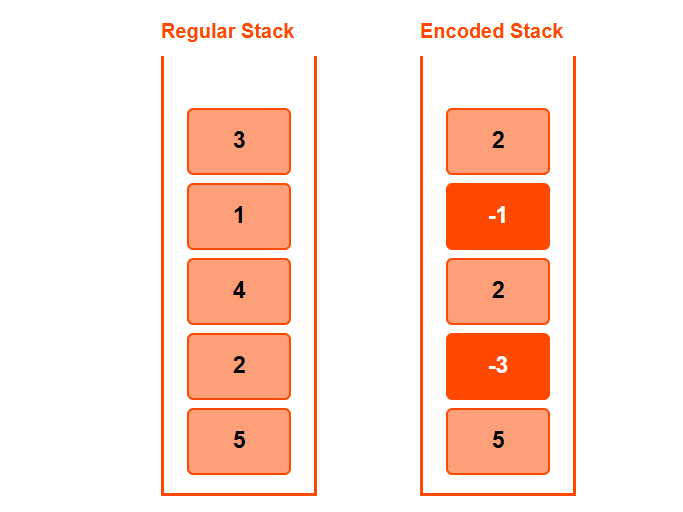
Now begin popping:
➤ pop()
- Pop 2 → it's positive
- So value removed = min_val + diff = 1 + 2 = 3
- min_val remains 1
stack = [0, -3, 2, -1], min_val = 1
➤ pop()
- Pop -1 → negative (we're removing the current minimum)
- Previous min = min_val - diff = 1 - (-1) = 2
- Update min_val = 2
stack = [0, -3, 2], min_val = 2
So even when the minimum is removed, it is restored from the diff!
Design Stack with O(1) getMin() Visualization
<visualization-box>
Code (Python)
class MinStack:
def __init__(self):
self.stack = []
self.min_val = float('inf')
def push(self, val: int) -> None:
if not self.stack:
self.stack.append(0)
self.min_val = val
else:
diff = val - self.min_val
self.stack.append(diff)
if diff < 0:
self.min_val = val
def pop(self) -> None:
if not self.stack:
return
diff = self.stack.pop()
if diff < 0:
prev_min = self.min_val
self.min_val = prev_min - diff
return prev_min
else:
return self.min_val + diff
def top(self) -> int:
if not self.stack:
return -1
top_diff = self.stack[-1]
if top_diff < 0:
return self.min_val
else:
return self.min_val + top_diff
def getMin(self) -> int:
if not self.stack:
return -1
return self.min_val
Code (C++)
#include <stack>
#include <climits>
class MinStack {
private:
std::stack<long long> stack;
long long min_val;
public:
MinStack() {
min_val = LLONG_MAX;
}
void push(int val) {
if (stack.empty()) {
stack.push(0);
min_val = val;
} else {
long long diff = (long long)val - min_val;
stack.push(diff);
if (diff < 0) {
min_val = val;
}
}
}
void pop() {
if (stack.empty()) return;
long long diff = stack.top();
stack.pop();
if (diff < 0) {
min_val = min_val - diff;
}
}
int top() {
if (stack.empty()) return -1;
long long diff = stack.top();
if (diff < 0) {
return min_val;
} else {
return min_val + diff;
}
}
int getMin() {
if (stack.empty()) return -1;
return min_val;
}
};
Code (Java)
import java.util.Stack;
class MinStack {
private Stack<Long> stack;
private long minVal;
public MinStack() {
stack = new Stack<>();
minVal = Long.MAX_VALUE;
}
public void push(int val) {
if (stack.isEmpty()) {
stack.push(0L);
minVal = val;
} else {
long diff = (long)val - minVal;
stack.push(diff);
if (diff < 0) {
minVal = val;
}
}
}
public void pop() {
if (stack.isEmpty()) return;
long diff = stack.pop();
if (diff < 0) {
minVal = minVal - diff;
}
}
public int top() {
if (stack.isEmpty()) return -1;
long diff = stack.peek();
if (diff < 0) {
return (int)minVal;
} else {
return (int)(minVal + diff);
}
}
public int getMin() {
if (stack.isEmpty()) return -1;
return (int)minVal;
}
}
Conclusion
In this article, we explored how to design a stack that supports finding the minimum element in constant time without using additional space. We started with a brute force approach using extra space, then developed an optimized solution that encodes minimum information within the stack itself.
The key to this problem is recognizing that we can store differences rather than actual values, which allows us to track the minimum element without additional data structures. This technique of encoding extra information in existing structures is a powerful concept in algorithm design.
This problem demonstrates that by thinking creatively about data representation, we can often find ways to improve time and space complexity beyond what initially seems possible.
