Subarray with Given Sum: Codes with Visualization
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
Problem Statement
Given an array of non-negative integers and a target sum, we need to find a continuous subarray that adds up to the given target sum. If such a subarray exists, we should return the starting and ending positions of the first such subarray found. If no such subarray exists, we return that the subarray wasn't found.
For example:
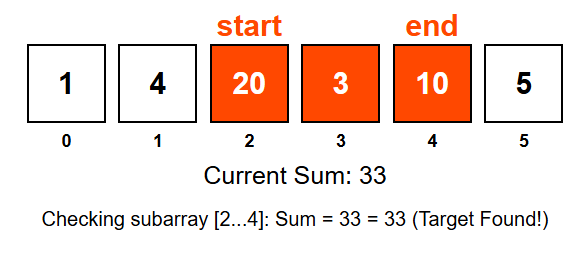
- Input: array = [1, 4, 20, 3, 10, 5], target sum = 33
- Output: Subarray found from index 2 to 4 (20 + 3 + 10 = 33)
Brute Force Approach
Explanation
The simplest way to solve this problem is to check every possible subarray. For each starting position, we try all possible ending positions and check if the sum equals our target.
This approach involves two nested loops:
- The outer loop selects the starting position
- The inner loop considers all possible ending positions from that start
- For each subarray, we calculate the sum and check if it matches our target
While this method always works, it's not efficient for large arrays because we examine every possible subarray.
Time Complexity: O(n²) - we have nested loops
Space Complexity: O(1) - we only use a few variables regardless of input size
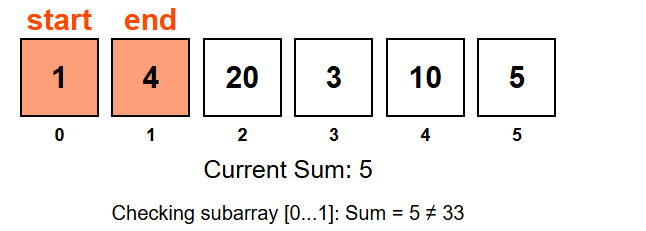
Here Start Index is 0 and end index is 1 so Sum = 1 + 4 = 5, Next iteration end will increase, continue upto end index is less than 6
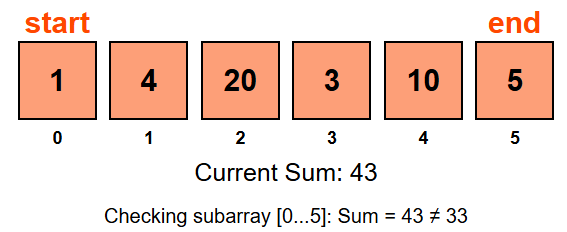
Here end index has reached 5 , after this sum will be reset to zero, the start index will move to index 1, and the process will repeat until the start index reaches the end
For example
Code (Python)
def subarray_sum_brute_force(arr, target_sum):
n = len(arr)
# Check all possible subarrays
for start in range(n):
current_sum = 0
for end in range(start, n):
current_sum += arr[end]
# If current sum equals target sum, we found our subarray
if current_sum == target_sum:
return (start, end)
# If we reach here, no subarray with given sum exists
return "No subarray found with the given sum"
Code (C++)
string subarray_sum_brute_force(vector<int>& arr, int target_sum) {
int n = arr.size();
// Check all possible subarrays
for (int start = 0; start < n; start++) {
int current_sum = 0;
for (int end = start; end < n; end++) {
current_sum += arr[end];
// If current sum equals target sum, we found our subarray
if (current_sum == target_sum) {
return "Subarray found from index " + to_string(start) + " to " + to_string(end);
}
}
}
// If we reach here, no subarray with given sum exists
return "No subarray found with the given sum";
}
Code (Java)
public static String subarraySumBruteForce(int[] arr, int targetSum) {
int n = arr.length;
// Check all possible subarrays
for (int start = 0; start < n; start++) {
int currentSum = 0;
for (int end = start; end < n; end++) {
currentSum += arr[end];
// If current sum equals target sum, we found our subarray
if (currentSum == targetSum) {
return "Subarray found from index " + start + " to " + end;
}
}
}
// If we reach here, no subarray with given sum exists
return "No subarray found with the given sum";
}
Optimized Approach
Explanation
We can solve this problem more efficiently using a sliding window technique. Since all numbers in the array are non-negative, the sum of elements can only increase as we add more elements.
The optimized algorithm works like this:
- Start with an empty window (both start and end at index 0)
- Keep adding elements to the window (by moving the end pointer) until the sum becomes greater than or equal to the target
- If the sum exceeds the target, start removing elements from the beginning (by moving the start pointer) until the sum becomes less than or equal to the target
- If at any point the sum equals the target, we've found our answer
This approach is much more efficient because we examine each element at most twice - once when adding it to the window and once when removing it.
Time Complexity: O(n) - linear time as we process each array element at most twice
Space Complexity: O(1) - we only use a few variables regardless of input size
Consider the example array: [1, 4, 20, 3, 10, 5]. Initially, both the start and end pointers are at index 0, and the sum is zero.
As we iterate through the array with the end pointer, once end reaches index 4, the sum becomes 38, which is greater than the target sum of 33.
At this point, we begin shrinking the window by incrementing the start pointer and removing elements from the beginning of the window, until the sum is less than or equal to 33
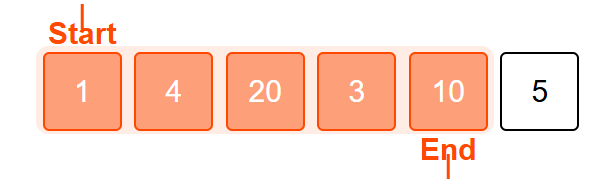
Current sum (38) is greater than our target (33)
Start Shrinking.
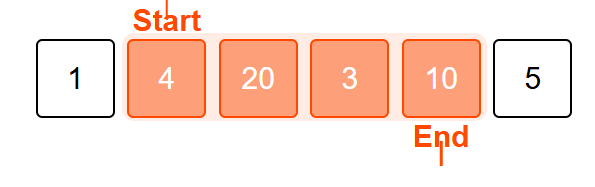
Current sum (38) is greater than our target (33)
Continue shrinking
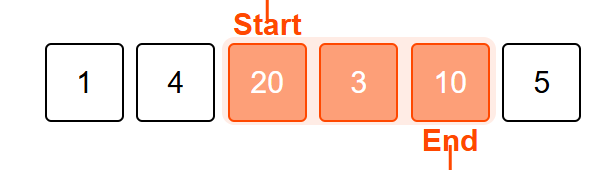
Current sum (33) is equal to our target (33).
Stop shrinking
Subarray with Given Sum Visualization
<visualization-box>
Code (Python)
def subarray_sum_optimized(arr, target_sum):
n = len(arr)
current_sum = arr[0]
start = 0
# Handle case where first element equals target sum
if current_sum == target_sum:
return (0, 0)
# Try to find subarray with sum equal to target_sum
for end in range(1, n):
# Add current element to sum
current_sum += arr[end]
# If sum becomes greater than target, remove elements from the beginning
while current_sum > target_sum and start < end:
current_sum -= arr[start]
start += 1
# Check if current sum equals target sum
if current_sum == target_sum:
return (start, end)
# If we reach here, no subarray with given sum exists
return "No subarray found with the given sum"
Code (C++)
string subarray_sum_optimized(vector<int>& arr, int target_sum) {
int n = arr.size();
if (n == 0) {
return "Array is empty";
}
int current_sum = arr[0];
int start = 0;
if (current_sum == target_sum) {
return "Subarray found from index 0 to 0";
}
for (int end = 1; end < n; end++) {
current_sum += arr[end];
while (current_sum > target_sum && start < end) {
current_sum -= arr[start];
start++;
}
if (current_sum == target_sum) {
return "Subarray found from index " + to_string(start) + " to " + to_string(end);
}
}
return "No subarray found with the given sum";
}
Code (Java)
public static String subarraySumOptimized(int[] arr, int targetSum) {
int n = arr.length;
if (n == 0) {
return "Array is empty";
}
int currentSum = arr[0];
int start = 0;
if (currentSum == targetSum) {
return "Subarray found from index 0 to 0";
}
for (int end = 1; end < n; end++) {
currentSum += arr[end];
while (currentSum > targetSum && start < end) {
currentSum -= arr[start];
start++;
}
if (currentSum == targetSum) {
return "Subarray found from index " + start + " to " + end;
}
}
return "No subarray found with the given sum";
}
Conclusion
In this article, we tackled the "Subarray with Given Sum" problem using two different approaches:
1. The brute force method checks all possible subarrays but runs in O(n²) time.
2. The optimized sliding window technique achieves a much better O(n) time complexity.
The sliding window approach shows how we can transform a quadratic solution into a linear one by avoiding redundant calculations. This technique is valuable for many array-based problems and shows how thinking about the properties of your data (in this case, non-negative integers) can lead to significant performance gains.
