Sliding Window Algorithm Explained (Code with Animation)

Written by

Sasank Nasika

Edited by

Kaustubh Saini

Last updated on

May 12, 2025

In this blog, we'll dive into Sliding Window, exploring its core concepts, implementation strategies, and how to tackle common problems using it effectively.

Sliding Window Algorithm Explained (Code with Animation)

Fundamentals of Sliding Window

Basic Concept and Visual Representation

Think of the sliding window as a frame that moves across your data. As the frame slides, you can:

Add elements as they enter the window
Remove elements as they exit the window
Track information about the current window contents

Let's visualize this with a simple array: [1,3,2,6,4,8,5]

With a window size of 3:

Initial window: [1,3,2]

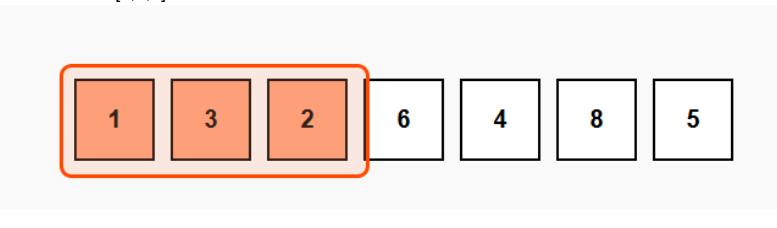
Slide right: [3,2,6]

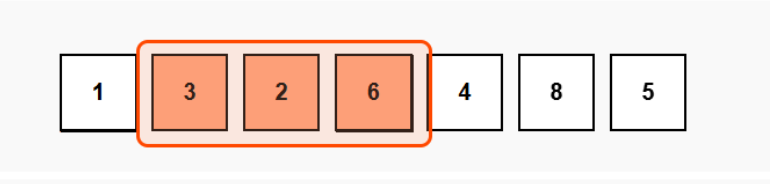
Slide right: [2,6,4]

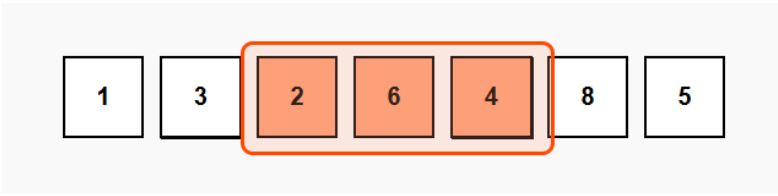
Slide right: [6,4,8]

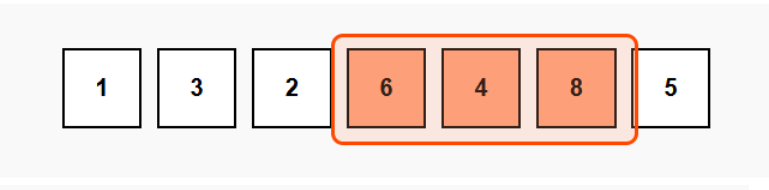
Slide right: [4,8,5]

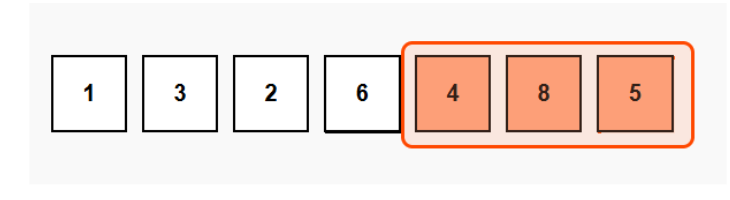
The key insight is that we don't need to recalculate everything when the window moves - we can update our results incrementally.

Sliding Window Algorithm Visualization

<visualization-box>

Fixed vs Dynamic Window Sizes

There are two main variations of the sliding window technique:

Fixed-size window: The window size remains constant throughout the algorithm. This is useful for problems like "find the maximum sum of a subarray of size k."

Dynamic-size window: The window can grow or shrink based on certain conditions. This is useful for problems like "find the smallest subarray with a sum greater than a target value."

Time Complexity Advantage

The sliding window approach achieves O(n) time complexity for many problems that would otherwise require O(n²) with naive approaches.

For example, if you want to find all subarrays of size k in an array of size n:

Brute force: Each subarray calculation requires k operations, and there are (n-k+1) subarrays, resulting in O(k × (n-k+1)) = O(n²) time complexity.
Sliding window: Only one pass through the array is needed, giving O(n) time complexity.

How the Sliding Window Works

Basic Steps of the Algorithm

The sliding window algorithm follows these general steps:

Initialize a window (typically with pointers)
Process the elements within the current window
Slide the window (expand or contract based on the problem)
Update the result based on the current window
Repeat until the end of the data structure is reached

Setting Window Boundaries

We typically use two pointers to define the window:

left (or start): Points to the beginning of the window
right (or end): Points to the end of the window

These pointers help us track which elements are currently in our window.

Expanding the Window

When we need to include more elements in our window, we increase the right pointer. This usually happens when:

We're looking for a longer sequence
The current window doesn't meet our criteria
We're processing a fixed-size window and moving to the next position

Contracting the Window

When we need to remove elements from our window, we increase the left pointer. This usually happens when:

Our window has grown too large
The window contains elements that violate our criteria
We're maintaining a fixed-size window and need to move forward

Repeating Until Completion

The algorithm continues expanding and contracting the window until the right pointer reaches the end of the array/string.

Code Implementation

Let's implement solutions for a common sliding window problem: finding the maximum sum of a subarray of size k.

Python Implementation

def max_sum_subarray(arr, k):
    # Input validation
    if len(arr) < k:
        return "Array size is less than window size"
    
    # Calculate sum of first window
    window_sum = sum(arr[:k])
    max_sum = window_sum
    
    # Slide the window and update max_sum
    for i in range(k, len(arr)):
        # Add the incoming element and remove the outgoing element
        window_sum = window_sum + arr[i] - arr[i - k]
        # Update maximum sum if current window sum is greater
        max_sum = max(max_sum, window_sum)
    
    return max_sum

# Example usage
array = [2, 1, 5, 1, 3, 2]
k = 3
print(f"Maximum sum of subarray of size {k}: {max_sum_subarray(array, k)}")  # Output: 9

C++ Implementation

#include <iostream>
#include <vector>
#include <algorithm>

int maxSumSubarray(const std::vector<int>& arr, int k) {
    // Input validation
    if (arr.size() < k) {
        std::cout << "Array size is less than window size" << std::endl;
        return -1;
    }
    
    // Calculate sum of first window
    int windowSum = 0;
    for (int i = 0; i < k; i++) {
        windowSum += arr[i];
    }
    
    int maxSum = windowSum;
    
    // Slide the window and update maxSum
    for (int i = k; i < arr.size(); i++) {
        // Add the incoming element and remove the outgoing element
        windowSum = windowSum + arr[i] - arr[i - k];
        // Update maximum sum if current window sum is greater
        maxSum = std::max(maxSum, windowSum);
    }
    
    return maxSum;
}

int main() {
    std::vector<int> array = {2, 1, 5, 1, 3, 2};
    int k = 3;
    std::cout << "Maximum sum of subarray of size " << k << ": " 
              << maxSumSubarray(array, k) << std::endl;  // Output: 9
    return 0;
}

Java Implementation

public class SlidingWindow {
    public static int maxSumSubarray(int[] arr, int k) {
        // Input validation
        if (arr.length < k) {
            System.out.println("Array size is less than window size");
            return -1;
        }
        
        // Calculate sum of first window
        int windowSum = 0;
        for (int i = 0; i < k; i++) {
            windowSum += arr[i];
        }
        
        int maxSum = windowSum;
        
        // Slide the window and update maxSum
        for (int i = k; i < arr.length; i++) {
            // Add the incoming element and remove the outgoing element
            windowSum = windowSum + arr[i] - arr[i - k];
            // Update maximum sum if current window sum is greater
            maxSum = Math.max(maxSum, windowSum);
        }
        
        return maxSum;
    }
    
    public static void main(String[] args) {
        int[] array = {2, 1, 5, 1, 3, 2};
        int k = 3;
        System.out.println("Maximum sum of subarray of size " + k + ": " + 
                           maxSumSubarray(array, k));  // Output: 9
    }
}

Window Building Process

The window building process typically follows these steps:

Initialize the window with the first elements (if fixed size) or start with an empty window
Process the window according to the problem requirements
Update any tracking variables (like max_sum, min_length, etc.)
Slide the window to the next position

Window Transition Mechanism

When transitioning from one window to the next, we:

Add new elements that enter the window
Remove elements that exit the window
Update any calculations for the new window

This is more efficient than recalculating everything for each new window position.

Sliding Window Trick for Efficient Transitions

The key trick for efficiency is to update values incrementally. For example, in our maximum sum problem:

Instead of recalculating the entire sum: window_sum = sum(arr[i:i+k])
We use: window_sum = window_sum + arr[i] - arr[i-k]

This reduces the work from O(k) operations to O(1) operations per window transition.

Common Applications Of Sliding Window

Goal:

Counting Subarrays that satisfy a given condition (e.g., sum ≤ K, all elements unique, etc.).
Finding the minimum or maximum length subarray that satisfies a condition (e.g., sum ≥ K).

Initialize two pointers: left = 0 and right = 0.

Initialize necessary tracking variables: for example, sum = 0, count = 0, minLength = ∞ (or maxLength = 0).

Start a loop where right goes from 0 to end of array.

Add nums[right] to the tracking variable (e.g., add to sum).

While the current window does not satisfy the condition, move left to the right and update the tracking variable (e.g., subtract nums[left] from sum)

When the window does satisfy the condition:

For counting subarrays: add (right - left + 1) to count.
For min/max length: update minLength or maxLength using (right - left + 1).

Move right to the next index and repeat steps 4–6.

After the loop ends, return the result: count, minLength, or maxLength based on the problem.

Below Are Some Standard Problems.

Count the number of subarrays (contiguous segments) whose sum is less than or equal to K.

function countSubarrays(nums, K):
    left = 0
    sum = 0
    count = 0

    for right from 0 to length of nums - 1:
        sum += nums[right]

        while sum > K:
            sum -= nums[left]
            left += 1

        // All subarrays ending at 'right' and starting from 'left' to 'right' are valid
        count += (right - left + 1)

    return count

Finding Subarray with Minimum Length and Sum ≥ N

This is a classic dynamic window problem

function minSubarrayWithSumGreaterThan(arr, target):
    left = 0
    current_sum = 0
    min_length = ∞
    for right from 0 to length(arr) - 1:
        current_sum += arr[right]
        while current_sum ≥ target:
            min_length = min(min_length, right - left + 1)
            current_sum -= arr[left]
            left += 1
    if min_length == ∞:
        return 0
    else: return min_length

Finding Longest Substring Without Repeating Characters

Another common sliding window problem

def longest_substring_without_repeating(s):
    char_map = {}  # Track character positions
    left = 0
    max_length = 0
    
    for right in range(len(s)):
        # If character is already in the window and its position is >= left
        if s[right] in char_map and char_map[s[right]] >= left:
            # Move left pointer to position after the repeated character
            left = char_map[s[right]] + 1
        else:
            # Update max length
            max_length = max(max_length, right - left + 1)
        
        # Update character position
        char_map[s[right]] = right
    
    return max_length

Analyzing Fixed Periods in Data Sequences

The sliding window technique is perfect for analyzing data over fixed periods, like calculating moving averages

def moving_average(data, window_size):
    results = []
    window_sum = sum(data[:window_size])
    results.append(window_sum / window_size)
    
    for i in range(window_size, len(data)):
        window_sum = window_sum + data[i] - data[i - window_size]
        results.append(window_sum / window_size)
    
    return results

Algorithm Comparison

Sliding Window vs Traditional Approaches

When to Use Sliding Window

The sliding window technique is ideal for problems with these characteristics:

You're processing a linear data structure (array, string, linked list)
You need to find a substructure (subarray, substring) that meets certain criteria
The problem involves consecutive elements
You need to minimize computations when the window moves

Common problem patterns include:

Finding max/min sum of a subarray of size k
Finding shortest/longest subarray meeting certain conditions
Finding all subarrays that meet specific criteria

Optimizations

Some optimizations for sliding window algorithms include:

Early termination when conditions can't be met
Using appropriate data structures for window tracking
Preprocessing input when possible
Pre-calculating cumulative sums for faster window sum calculations

Common Mistakes

Incorrect pointer initialization
Starting left or right at the wrong index (for example –1 instead of 0) shifts every window and breaks the logic.
Off‑by‑one in window bounds
Mixing inclusive vs. exclusive ends—decide if your window is [left…right] or [left…right) and apply it consistently.
Recomputing the whole window on each step
Summing or scanning the entire window every time instead of adding/subtracting the entering/exiting element destroys the O(N) performance.
Forgetting the final window check
In min‑size or max‑size problems, you must handle windows that become valid only at the very end of the iteration.
Failing to update auxiliary data structures
When using a map or set for counts, always decrement or remove entries as you move left forward, or your condition checks will be wrong.
Ignoring edge cases
Don’t forget empty arrays, arrays where every element already satisfies (or never satisfies) the condition, or targets of zero—these often need explicit handling.
Assuming monotonicity that doesn’t exist
Sliding‑window only works when expanding always “improves” (or always “worsens”) the condition. If adding or removing elements can swing your condition both ways unpredictably, you need a different technique.

Key Takeaways

The sliding window algorithm is a powerful technique for solving array and string problems with improved efficiency. Key points to remember:
1. Sliding window reduces time complexity from O(n²) to O(n) for many problems.
2. There are two types: fixed-size windows and dynamic-size windows.
3. The technique avoids recalculating information by making incremental updates.
4. It's especially useful for finding subarrays or substrings that meet specific criteria.

FAQs

Compare

vs InterviewCopilot.io

vs Interviews.chat

vs PrepAI

Resources

Blog

Success Stories

Help Center

Legal

Terms & Conditions

Cookie Policy

GDPR