Equilibrium Index in Arrays: Codes with Visualization

Problem Statement
In an array, an equilibrium index is a position where the sum of all elements to the left equals the sum of all elements to the right.
More formally, for an array A with n elements, index i is an equilibrium index if:
- Sum of elements A[0] to A[i-1] equals sum of elements A[i+1] to A[n-1]
- Note: If i = 0, the left sum is considered 0
- Note: If i = n-1, the right sum is considered 0
For example, in the array [4, 2, 2, 4, 5, 1], the equilibrium index is 3 because:
- Sum of elements to the left of index 3 (A[0] + A[1] + A[2]) = 4 + 2 + 2 = 8
- Sum of elements to the right of index 3 (A[4] + A[5]) = 5 + 3 = 8
Our task is to find an equilibrium index if it exists, or return -1 if there isn't one.
Brute Force Approach
Explanation
The simplest way to solve this problem is to check each index of the array:
- For each index i, calculate the sum of elements to its left
- Calculate the sum of elements to its right
- Compare the two sums - if they're equal, return i
This approach is straightforward but involves recalculating sums for each index.
Time Complexity: O(n²) where n is the length of the array
Space Complexity: O(1) as we only use a few variables
Let's Consider the array [4 2 2 4 5 3]
Step 1: i = 0
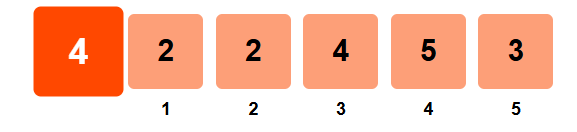
- left_sum = 0 (no elements on the left)
- right_sum = 2 + 2 + 4 + 5 + 3 = 16
- left_sum ≠ right_sum → not equilibrium
Step 2: i = 1
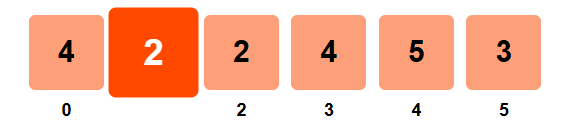
- left_sum = 4
- right_sum = 2 + 4 + 5 + 3 = 14
- left_sum ≠ right_sum → not equilibrium
Step 3: i = 2
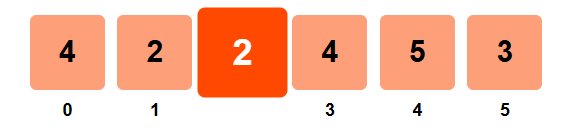
- left_sum = 4 + 2 = 6
- right_sum = 4 + 5 + 3 = 12
- left_sum ≠ right_sum → not equilibrium
Step 4: i = 3
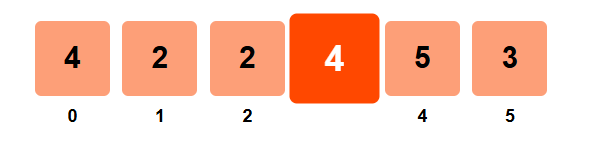
- left_sum = 4 + 2 + 2 = 8
- right_sum = 5 + 3 = 8
- left_sum = right_sum = 8 → Equilibrium index found!
Code (Python)
def find_equilibrium_index_brute_force(arr):
n = len(arr)
for i in range(n):
# Calculate sum of elements to the left of index i
left_sum = 0
for j in range(i):
left_sum += arr[j]
# Calculate sum of elements to the right of index i
right_sum = 0
for j in range(i + 1, n):
right_sum += arr[j]
# Check if this is an equilibrium index
if left_sum == right_sum:
return i
# No equilibrium index found
return -1
Code (C++)
int findEquilibriumIndexBruteForce(const std::vector<int>& arr) {
int n = arr.size();
for (int i = 0; i < n; i++) {
// Calculate sum of elements to the left of index i
int leftSum = 0;
for (int j = 0; j < i; j++) {
leftSum += arr[j];
}
// Calculate sum of elements to the right of index i
int rightSum = 0;
for (int j = i + 1; j < n; j++) {
rightSum += arr[j];
}
// Check if this is an equilibrium index
if (leftSum == rightSum) {
return i;
}
}
// No equilibrium index found
return -1;
}
Code (Java)
public static int findEquilibriumIndexBruteForce(int[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) {
// Calculate sum of elements to the left of index i
int leftSum = 0;
for (int j = 0; j < i; j++) {
leftSum += arr[j];
}
// Calculate sum of elements to the right of index i
int rightSum = 0;
for (int j = i + 1; j < n; j++) {
rightSum += arr[j];
}
// Check if this is an equilibrium index
if (leftSum == rightSum) {
return i;
}
}
// No equilibrium index found
return -1;
}
Optimized Approach
Explanation
We can optimize our solution by avoiding recalculating sums for each index. The key insight is to:
- Calculate the total sum of the array once
- Keep track of a running sum from left to right
- At each index, the right sum can be calculated as: (total sum - current element - left sum)
- If left sum equals right sum at any point, we've found our equilibrium index
This approach reduces our time complexity significantly.
Time Complexity: O(n) where n is the length of the array
Space Complexity: O(1) as we only use a few variables
Consider the Example Array [4 2 2 4 5 3]:
Let's Initialize some variables, total_sum = 4 + 2 + 2 + 4 + 5 + 3 = 20 , left_sum = 0
Step 1: i = 0, arr[0] = 4
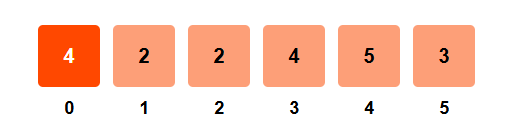
- right_sum = 20 - 4 - 0 = 16
- left_sum = 0
- left_sum ≠ right_sum → not equilibrium
- Update left_sum = 0 + 4 = 4
Step 2: i = 1, arr[1] = 2
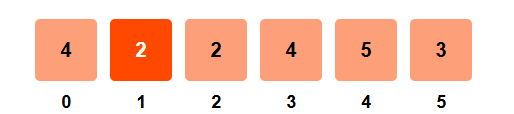
- right_sum = 20 - 2 - 4 = 14
- left_sum = 4
- left_sum ≠ right_sum
- Update left_sum = 4 + 2 = 6
Step 3: i = 2, arr[2] = 2
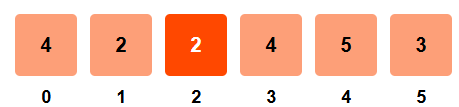
- right_sum = 20 - 2 - 6 = 12
- left_sum = 6
- left_sum ≠ right_sum
- Update left_sum = 6 + 2 = 8
Step 4: i = 3, arr[3] = 4
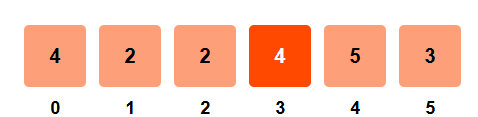
- right_sum = 20 - 4 - 8 = 8
- left_sum = 8
- left_sum == right_sum → Equilibrium index found!
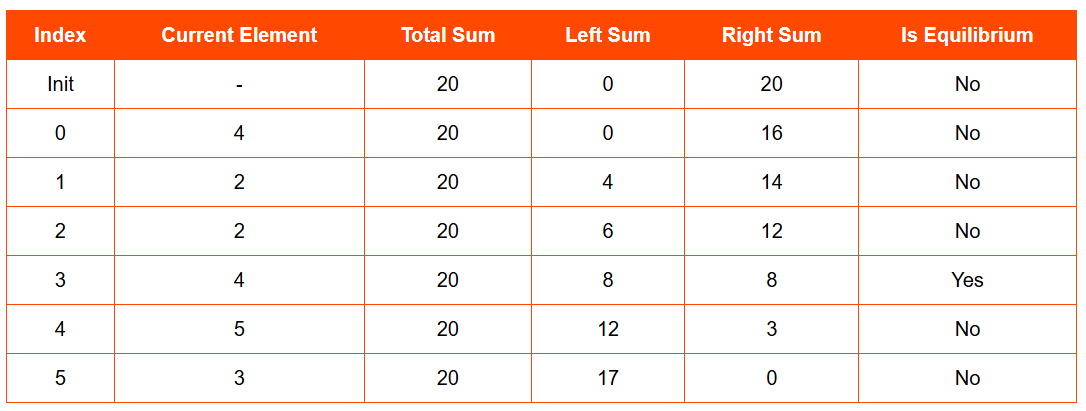
Equilibrium Index in Array Visualization
<visualization-box>
Code (Python)
def find_equilibrium_index_optimized(arr):
n = len(arr)
# Calculate total sum of the array
total_sum = sum(arr)
# Initialize left sum to 0
left_sum = 0
for i in range(n):
# Right sum = total sum - current element - left sum
right_sum = total_sum - arr[i] - left_sum
# Check if this is an equilibrium index
if left_sum == right_sum:
return i
# Update left sum for next iteration
left_sum += arr[i]
# No equilibrium index found
return -1
Code (C++)
int findEquilibriumIndexOptimized(const std::vector<int>& arr) {
int n = arr.size();
// Calculate total sum of the array
int totalSum = std::accumulate(arr.begin(), arr.end(), 0);
// Initialize left sum to 0
int leftSum = 0;
for (int i = 0; i < n; i++) {
// Right sum = total sum - current element - left sum
int rightSum = totalSum - arr[i] - leftSum;
// Check if this is an equilibrium index
if (leftSum == rightSum) {
return i;
}
// Update left sum for next iteration
leftSum += arr[i];
}
// No equilibrium index found
return -1;
}
Code (Java)
public static int findEquilibriumIndexOptimized(int[] arr) {
int n = arr.length;
// Calculate total sum of the array
int totalSum = 0;
for (int num : arr) {
totalSum += num;
}
// Initialize left sum to 0
int leftSum = 0;
for (int i = 0; i < n; i++) {
// Right sum = total sum - current element - left sum
int rightSum = totalSum - arr[i] - leftSum;
// Check if this is an equilibrium index
if (leftSum == rightSum) {
return i;
}
// Update left sum for next iteration
leftSum += arr[i];
}
// No equilibrium index found
return -1;
}Conclusion
We've explored two approaches to find the equilibrium index in an array:
1.Brute Force Approach: Simple but inefficient with O(n²) time complexity
2.Optimized Approach: Efficient solution with O(n) time complexity that avoids recalculating sums
The optimized solution shows how a small change in approach—precomputing the total sum and using running sums—can greatly improve performance. This problem teaches basic array manipulation and the importance of avoiding redundant calculations.

