Longest Valid Parentheses Substring: Codes with Visualization
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
Problem Statement
Given a string containing just the characters '(' and ')', find the length of the longest valid (well-formed) parentheses substring.
A valid parentheses string is one where every opening parenthesis '(' has a matching closing parenthesis ')' in the correct order.
Examples:
- Input: "(()" → Output: 2
Explanation: The longest valid parentheses substring is "()"
- Input: ")()())" → Output: 4
Explanation: The longest valid parentheses substring is "()()"
- Input: "" → Output: 0
Explanation: Empty string has no valid parentheses
Brute Force Approach
Explanation
The brute force approach checks every possible substring to see if it's valid. We:
- Generate all possible substrings of the input string
- Check each substring to determine if it has valid parentheses
- Keep track of the maximum length of valid substrings found
This approach is straightforward but inefficient for longer strings since we check many substrings multiple times.
Python
def longestValidParentheses(s):
max_length = 0
for i in range(len(s)):
for j in range(i + 2, len(s) + 1, 2): # Only even-length substrings
if isValid(s[i:j]):
max_length = max(max_length, j - i)
return max_length
def isValid(s):
stack = []
for char in s:
if char == '(':
stack.append(char)
elif stack and stack[-1] == '(':
stack.pop()
else:
return False
return len(stack) == 0
# Example usage
print(longestValidParentheses("(()")) # Output: 2
C++
#include <string>
#include <stack>
#include <algorithm>
using namespace std;
bool isValid(string s) {
stack<char> stk;
for (char c : s) {
if (c == '(') {
stk.push(c);
} else if (!stk.empty() && stk.top() == '(') {
stk.pop();
} else {
return false;
}
}
return stk.empty();
}
int longestValidParentheses(string s) {
int max_length = 0;
for (int i = 0; i < s.length(); i++) {
for (int j = i + 2; j <= s.length(); j += 2) {
if (isValid(s.substr(i, j - i))) {
max_length = max(max_length, j - i);
}
}
}
return max_length;
}
// Example usage
// int main() {
// string s = "(()";
// cout << longestValidParentheses(s); // Output: 2
// }
Java
import java.util.Stack;
public class Solution {
public int longestValidParentheses(String s) {
int maxLength = 0;
for (int i = 0; i < s.length(); i++) {
for (int j = i + 2; j <= s.length(); j += 2) {
if (isValid(s.substring(i, j))) {
maxLength = Math.max(maxLength, j - i);
}
}
}
return maxLength;
}
private boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for (char c : s.toCharArray()) {
if (c == '(') {
stack.push(c);
} else if (!stack.isEmpty() && stack.peek() == '(') {
stack.pop();
} else {
return false;
}
}
return stack.isEmpty();
}
// public static void main(String[] args) {
// Solution sol = new Solution();
// System.out.println(sol.longestValidParentheses("(()")); // Output: 2
// }
}
Optimized Approach
Explanation
We can solve this problem more efficiently using a stack or dynamic programming. I'll present the stack-based solution because it's more intuitive:
- We use a stack to keep track of the indices of parentheses
- We start by pushing -1 onto the stack as a base index
- For each character in the string:
- If it's an opening parenthesis '(', push its index onto the stack
- If it's a closing parenthesis ')', pop the top element from the stack
- If the stack becomes empty, push the current index
- If not, calculate length of current valid substring (current_index - stack.top())
- Keep track of the maximum length found
This solution works in a single pass through the string and has much better performance.
Lets Consider the string = “)()())”
We start with a stack containing -1. This helps calculate the length of valid substrings.
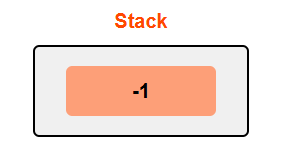
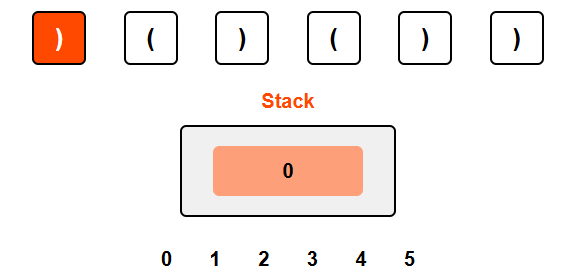
Processing ')': We encounter a closing parenthesis without a matching opening one. Pop -1 from the stack and push the current index 0.
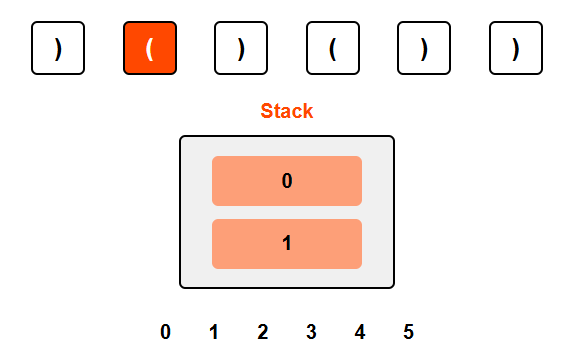
Processing '(': We push the current index 1 onto the stack.
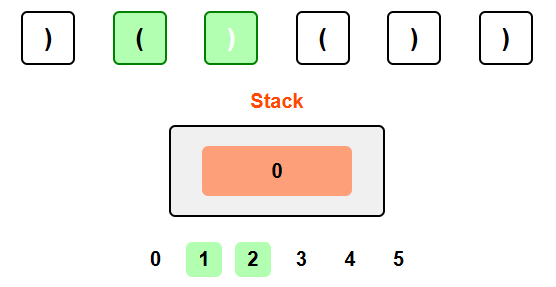
Processing ')': We found a matching pair! Pop index 1 from the stack. The valid substring length is (current index 2) - (top of stack 0) = 2.
Processing '(': We push the current index 3 onto the stack.
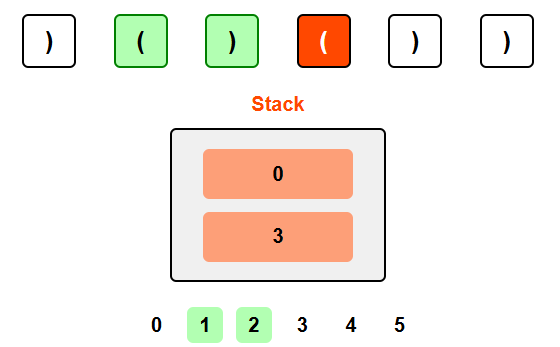
Processing ')': We found a matching pair! Pop index 3 from the stack. The valid substring length is (current index 4) - (top of stack 0) = 4.
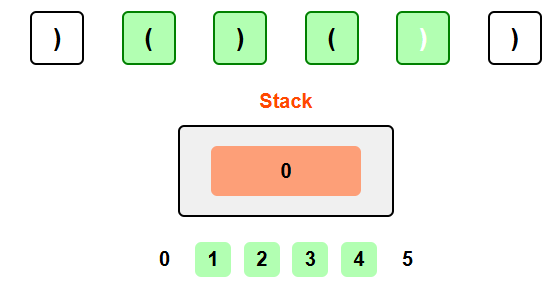
Processing ')': We encounter another closing parenthesis. Pop index 0 from the stack and push the current index 5.
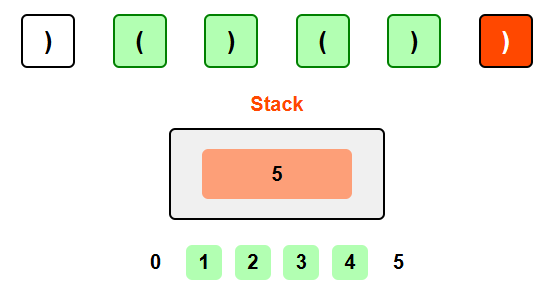
Final result: The longest valid substring has length 2 (characters at positions 1-2 or 3-4).
Longest Valid Parentheses Visualization
<visualization-box>
Python
def longestValidParentheses(s):
max_length = 0
stack = [-1] # Start with a base index
for i in range(len(s)):
if s[i] == '(':
stack.append(i)
else:
stack.pop()
if not stack:
stack.append(i)
else:
current_length = i - stack[-1]
max_length = max(max_length, current_length)
return max_length
# Example usage
# print(longestValidParentheses(")()())")) # Output: 4
C++
#include <string>
#include <stack>
#include <algorithm>
using namespace std;
int longestValidParentheses(string s) {
int max_length = 0;
stack<int> stk;
stk.push(-1); // Start with a base index
for (int i = 0; i < s.length(); i++) {
if (s[i] == '(') {
stk.push(i);
} else {
stk.pop();
if (stk.empty()) {
stk.push(i);
} else {
int current_length = i - stk.top();
max_length = max(max_length, current_length);
}
}
}
return max_length;
}
// Example usage
// int main() {
// string s = ")()())";
// cout << longestValidParentheses(s); // Output: 4
// }
Java
import java.util.Stack;
public class Solution {
public int longestValidParentheses(String s) {
int maxLength = 0;
Stack<Integer> stack = new Stack<>();
stack.push(-1); // Start with a base index
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else {
stack.pop();
if (stack.isEmpty()) {
stack.push(i);
} else {
int currentLength = i - stack.peek();
maxLength = Math.max(maxLength, currentLength);
}
}
}
return maxLength;
}
// public static void main(String[] args) {
// Solution sol = new Solution();
// System.out.println(sol.longestValidParentheses(")()())")); // Output: 4
// }
}
Conclusion
The "Length of the Longest Valid Substring" problem shows how we can move from a simple but inefficient brute force approach to an elegant, single-pass solution.
While the brute force method has a time complexity of O(n³) because we check O(n²) substrings and validation takes O(n) time, our optimized stack-based solution runs in just O(n) time with O(n) space complexity.
This problem highlights how data structures like stacks can help track matching pairs efficiently. The trick of using indices instead of characters in the stack is particularly clever, as it allows us to calculate valid substring lengths directly.
Learning to recognize these optimization patterns can help you solve many similar problems involving matching elements or keeping track of valid sequences.
