Remove Duplicates from Sorted Array (Solution With Visualization)
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
Problem Statement
Given a sorted array of integers, remove the duplicate elements such that each element appears only once. Return the new length of the modified array.
The array is already sorted in non-decreasing order, and you must modify the original array in-place. After removing duplicates, the first portion of the array should contain the unique elements in their original order, and you don't need to worry about what's left beyond the returned length.
For example:
- Input: [1, 1, 2]
- Output: [1,2]
- Input: [0, 0, 1, 1, 1, 2, 2, 3, 3, 4]
- Output: [0,1,2,3,4]
Brute Force Approach
Explanation
Since the array is sorted, all duplicates are adjacent.
In the brute force method:
- Start iterating from index 1.
- Compare the current element with the previous one.
- If they are equal, it's a duplicate:
- Shift all elements to the left starting from this position.
- Decrease the length by 1 (we "removed" an element).
- Else, move to the next index.
- Repeat until the entire array is processed
This approach has:
- Time Complexity: O(n) where n is the length of the array
- Space Complexity: O(1) as we modify the array in-place
Code (Python)
def removeDuplicates(nums):
n = len(nums)
i = 1
while i < n:
if nums[i] == nums[i - 1]:
# Shift elements to the left
for j in range(i, n - 1):
nums[j] = nums[j + 1]
n -= 1 # Reduce array size
else:
i += 1
return nCode (C++)
int removeDuplicates(vector<int>& nums) {
int n = nums.size();
for (int i = 1; i < n; ) {
if (nums[i] == nums[i - 1]) {
// Shift elements left
for (int j = i; j < n - 1; ++j)
nums[j] = nums[j + 1];
n--; // Reduce size
} else {
i++;
}
}
return n;
}
Code (Java)
public static int removeDuplicates(int[] nums) {
int n = nums.length;
int i = 1;
while (i < n) {
if (nums[i] == nums[i - 1]) {
// Shift elements left
for (int j = i; j < n - 1; j++) {
nums[j] = nums[j + 1];
}
n--; // Reduce size
} else {
i++;
}
}
return n;
}Optimized Approach
Explanation
Interestingly, the brute force approach is already quite efficient for this problem. Since we're dealing with a sorted array, we can identify duplicates with a single pass through the data. The approach above has a linear time complexity, which is optimal for this problem.
However, we can make a slight optimization by using a two-pointer technique to make the code more readable:
- Use two pointers: slow (points to the position where the next unique element should go) and fast (scans through the array)
- When fast finds a unique element (different from nums[slow-1]), copy it to the slow position and increment slow
- Continue until fast reaches the end of the array
- Return the array
This approach maintains:
- Time Complexity: O(n)
- Space Complexity: O(1)
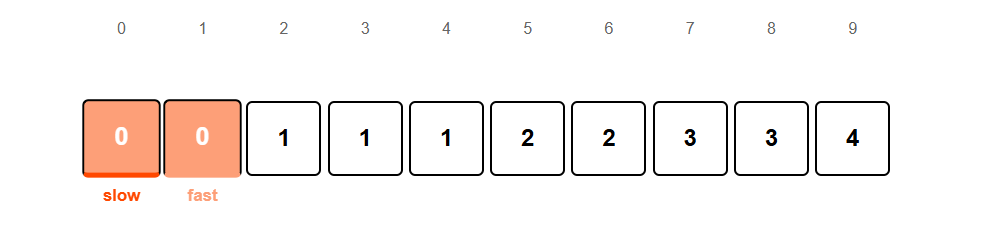
Comparing array[slow] = 0 with array[fast] = 0
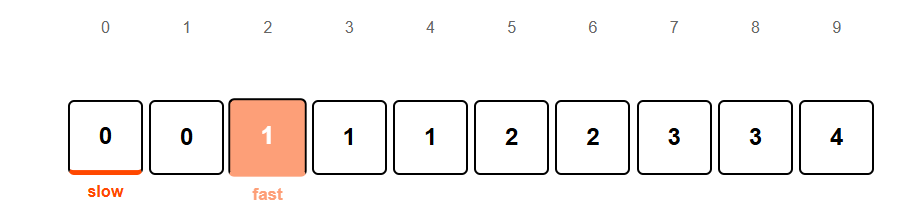
Moving fast pointer to index 2.
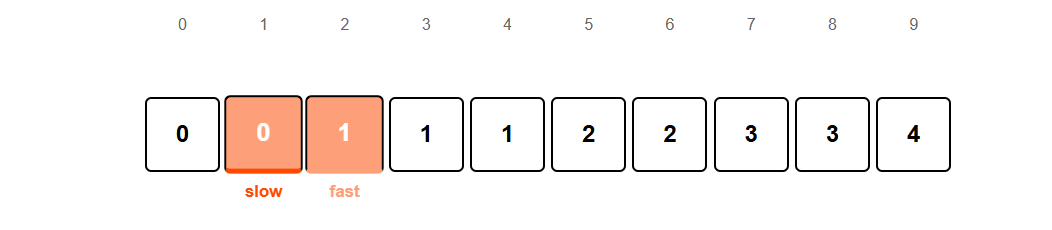
Comparing array[slow] = 0 with array[fast] = 1
Found a new unique element 1. Moving slow pointer to index 1.
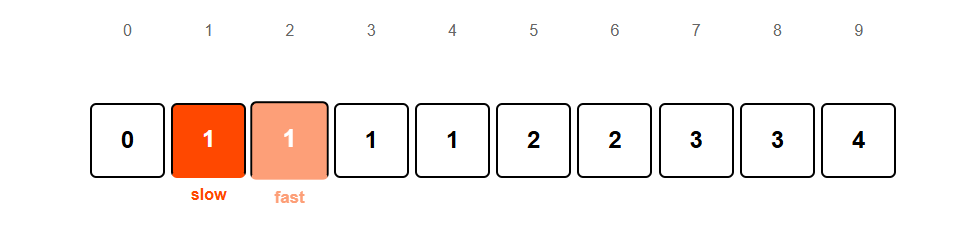
Placing the unique element 1 at position 1.
Repeating the Process Gives the final result
Remove Duplicates from Sorted Array Visualization
<visualization-box>
Code (Python)
def removeDuplicates(nums):
# Handle edge case of empty array
if not nums:
return 0
# Initialize slow pointer (position for next unique element)
slow = 1
# Fast pointer scans through the array
for fast in range(1, len(nums)):
# If current element is different from previous
if nums[fast] != nums[fast-1]:
# Place at the position indicated by slow
nums[slow] = nums[fast]
# Move slow pointer forward
slow += 1
# Return the count of unique elements
return slowCode (C++)
#include <vector>
int removeDuplicates(std::vector<int>& nums) {
// Handle edge case of empty array
if (nums.empty()) {
return 0;
}
// Initialize slow pointer (position for next unique element)
int slow = 1;
// Fast pointer scans through the array
for (int fast = 1; fast < nums.size(); fast++) {
// If current element is different from previous
if (nums[fast] != nums[fast-1]) {
// Place at the position indicated by slow
nums[slow] = nums[fast];
// Move slow pointer forward
slow++;
}
}
// Return the count of unique elements
return slow;
}Code (Java)
public int removeDuplicates(int[] nums) {
// Handle edge case of empty array
if (nums.length == 0) {
return 0;
}
// Initialize slow pointer (position for next unique element)
int slow = 1;
// Fast pointer scans through the array
for (int fast = 1; fast < nums.length; fast++) {
// If current element is different from previous
if (nums[fast] != nums[fast-1]) {
// Place at the position indicated by slow
nums[slow] = nums[fast];
// Move slow pointer forward
slow++;
}
}
// Return the count of unique elements
return slow;
}Conclusion
The "Remove Duplicates from Sorted Array" problem demonstrates how to efficiently process sorted data while modifying an array in-place.The brute force approach involves iterating through the array, shifting elements left when duplicates are found, with O(n²) time complexity and O(1) space. It’s easy but inefficient for large arrays. The optimal two-pointer method processes the array in a single pass, comparing elements with the last unique one and placing unique elements in place, with O(n) time complexity and O(1) space. The optimal approach is more efficient, making it ideal for real-world applications and larger datasets.
