Longest Consecutive Subsequence: Codes with Visualization

Problem Statement
Given an unsorted array of integers, find the length of the longest consecutive elements sequence.
For example, if the input array is [100, 4, 200, 1, 3, 2], the longest consecutive subsequence is [1, 2, 3, 4], so the output should be 4.
Important note: The algorithm should run in O(n) time complexity.

Brute Force Approach
Explanation
The simplest way to approach this problem is to:
- Sort the array
- Iterate through it, counting consecutive elements
While this isn't the most efficient solution, it's a good starting point to understand the problem.
After sorting, we can scan through the array and keep track of the current streak of consecutive numbers. Whenever we find a gap (current number is not one more than the previous), we reset our counter. We'll keep track of the maximum streak length we've seen so far.
Time Complexity: O(n log n) due to the sorting operation
Space Complexity: O(1) if we sort in place, or O(n) if we create a new sorted array
Python Code
def longest_consecutive_brute(nums):
if not nums:
return 0
# Sort the array
nums.sort()
longest_streak = 1
current_streak = 1
# Iterate through the sorted array
for i in range(1, len(nums)):
# If current element is different from previous (to handle duplicates)
if nums[i] != nums[i-1]:
# If current element is consecutive to previous
if nums[i] == nums[i-1] + 1:
current_streak += 1
else:
current_streak = 1
longest_streak = max(longest_streak, current_streak)
return longest_streak
C++ Code
#include <vector>
#include <algorithm>
int longestConsecutiveBrute(std::vector<int>& nums) {
if (nums.empty()) {
return 0;
}
std::sort(nums.begin(), nums.end());
int longest_streak = 1;
int current_streak = 1;
for (int i = 1; i < nums.size(); i++) {
if (nums[i] != nums[i-1]) {
if (nums[i] == nums[i-1] + 1) {
current_streak++;
} else {
current_streak = 1;
}
}
longest_streak = std::max(longest_streak, current_streak);
}
return longest_streak;
}
Java Code
import java.util.Arrays;
public class Solution {
public int longestConsecutiveBrute(int[] nums) {
if (nums.length == 0) {
return 0;
}
Arrays.sort(nums);
int longestStreak = 1;
int currentStreak = 1;
for (int i = 1; i < nums.length; i++) {
if (nums[i] != nums[i-1]) {
if (nums[i] == nums[i-1] + 1) {
currentStreak++;
} else {
currentStreak = 1;
}
}
longestStreak = Math.max(longestStreak, currentStreak);
}
return longestStreak;
}
}
Optimized Approach
Explanation
The brute force approach works, but it doesn't meet the O(n) time complexity requirement because of the sorting operation. We can do better using a HashSet.
The key insight is that we can use a set to quickly check if a number exists in our collection. Here's the optimized approach:
- Insert all elements of the array into a HashSet
- For each number in the array, check if it's the start of a sequence (i.e., if num-1 is not in the set)
- If it is a starting point, count how many consecutive elements follow it
- Keep track of the maximum sequence length
This approach works in O(n) time because:
- Building the HashSet takes O(n) time
- We do at most 2n lookups in the HashSet (checking for each number and its consecutive numbers)
- HashSet lookups are O(1) on average
Time Complexity: O(n)
Space Complexity: O(n) for the HashSet
Let's consider the array [100, 4, 200, 1, 3, 2].
num = 1
- 0 not in num_set → it's a sequence start
- current_num = 1, current_streak = 1
- 2 in num_set → current_num = 2, streak = 2
- 3 in num_set → current_num = 3, streak = 3
- 4 in num_set → current_num = 4, streak = 4
- 5 not in num_set → end sequence
longest_streak = max(0, 4) = 4
num = 2, 3, 4
- All of these have (num - 1) in the set → skip (not start of a new sequence)
num = 100
- 99 not in num_set → start of new sequence
- 101 not in num_set → streak = 1
longest_streak = max(4, 1) = 4 (unchanged)
num = 200
- 199 not in num_set → start of new sequence
- 201 not in num_set → streak = 1
longest_streak = max(4, 1) = 4 (unchanged)
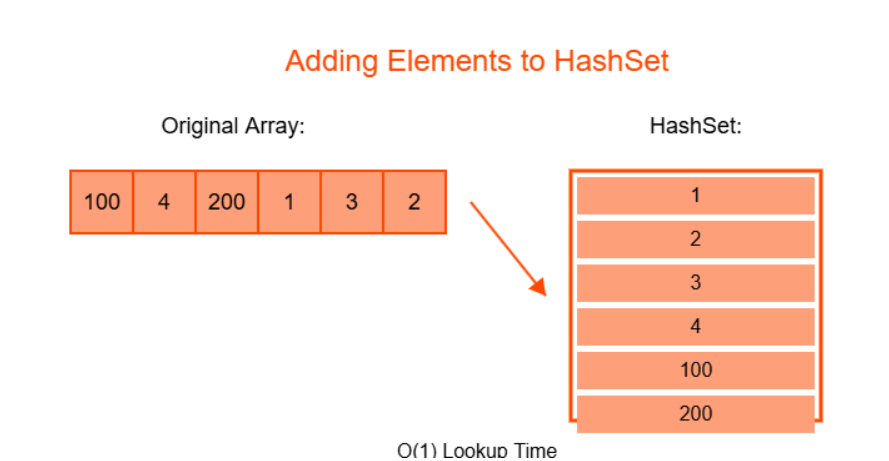
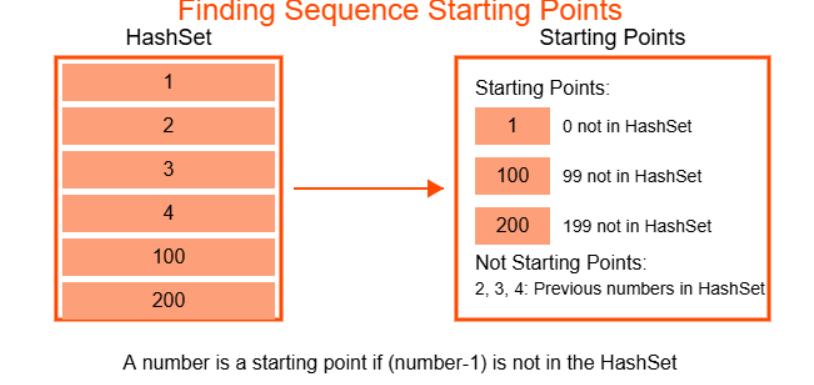
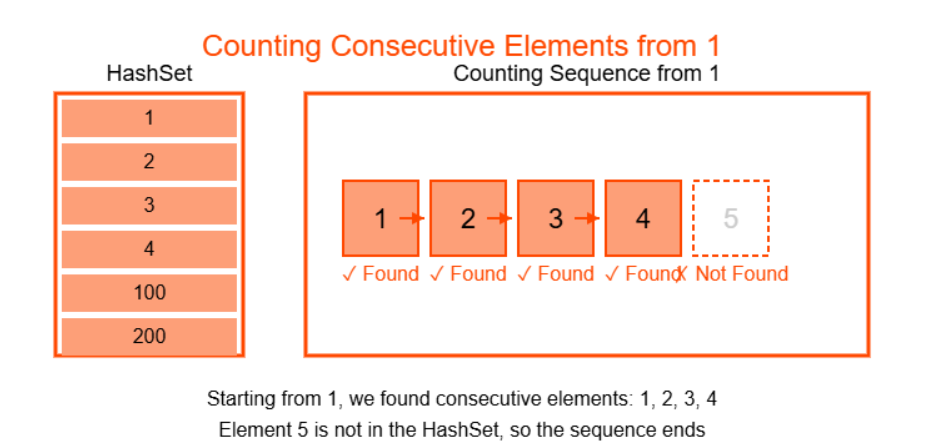
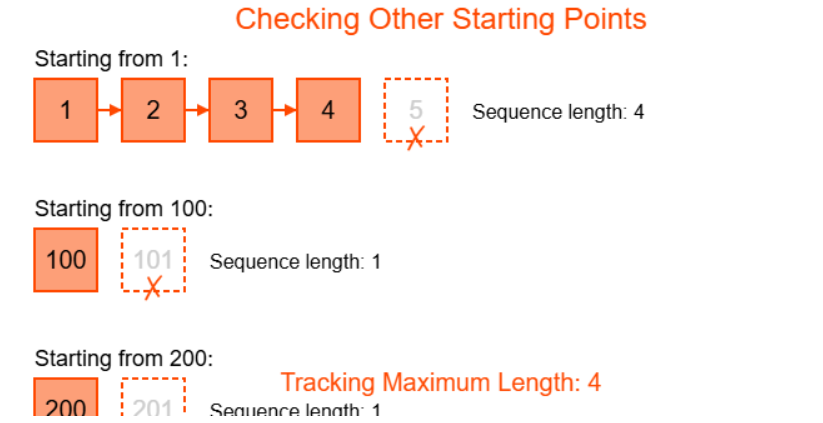
Longest Consecutive Subsequence Visualization
<visualization-box>
Python Code
def longest_consecutive(nums):
if not nums:
return 0
# Create a set of all numbers for O(1) lookups
num_set = set(nums)
longest_streak = 0
for num in num_set:
# Check if it's the start of a sequence
if num - 1 not in num_set:
current_num = num
current_streak = 1
# Count consecutive numbers
while current_num + 1 in num_set:
current_num += 1
current_streak += 1
longest_streak = max(longest_streak, current_streak)
return longest_streak
C++ Code
#include <vector>
#include <unordered_set>
#include <algorithm>
int longestConsecutive(std::vector<int>& nums) {
if (nums.empty()) return 0;
std::unordered_set<int> num_set(nums.begin(), nums.end());
int longest_streak = 0;
for (int num : num_set) {
if (num_set.find(num - 1) == num_set.end()) {
int current_num = num;
int current_streak = 1;
while (num_set.find(current_num + 1) != num_set.end()) {
current_num++;
current_streak++;
}
longest_streak = std::max(longest_streak, current_streak);
}
}
return longest_streak;
}
Java Code
import java.util.HashSet;
import java.util.Set;
public class Solution {
public int longestConsecutive(int[] nums) {
if (nums.length == 0) return 0;
Set<Integer> numSet = new HashSet<>();
for (int num : nums) {
numSet.add(num);
}
int longestStreak = 0;
for (int num : numSet) {
if (!numSet.contains(num - 1)) {
int currentNum = num;
int currentStreak = 1;
while (numSet.contains(currentNum + 1)) {
currentNum++;
currentStreak++;
}
longestStreak = Math.max(longestStreak, currentStreak);
}
}
return longestStreak;
}
}
Conclusion
In this article, we learned how to find the longest consecutive subsequence in an array. We started with a brute force approach using sorting, which gave us an O(n log n) solution. Then, we optimized it to an O(n) solution using a HashSet, meeting the problem's requirement.
The key takeaway from this problem is how using the right data structure can dramatically improve the efficiency of our algorithm. By using a HashSet to enable O(1) lookups, we transformed what would have been an O(n²) or O(n log n) problem into a linear time solution.

