Product of Array Except Self: Solution with Code (Visualization)
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
Problem Statement
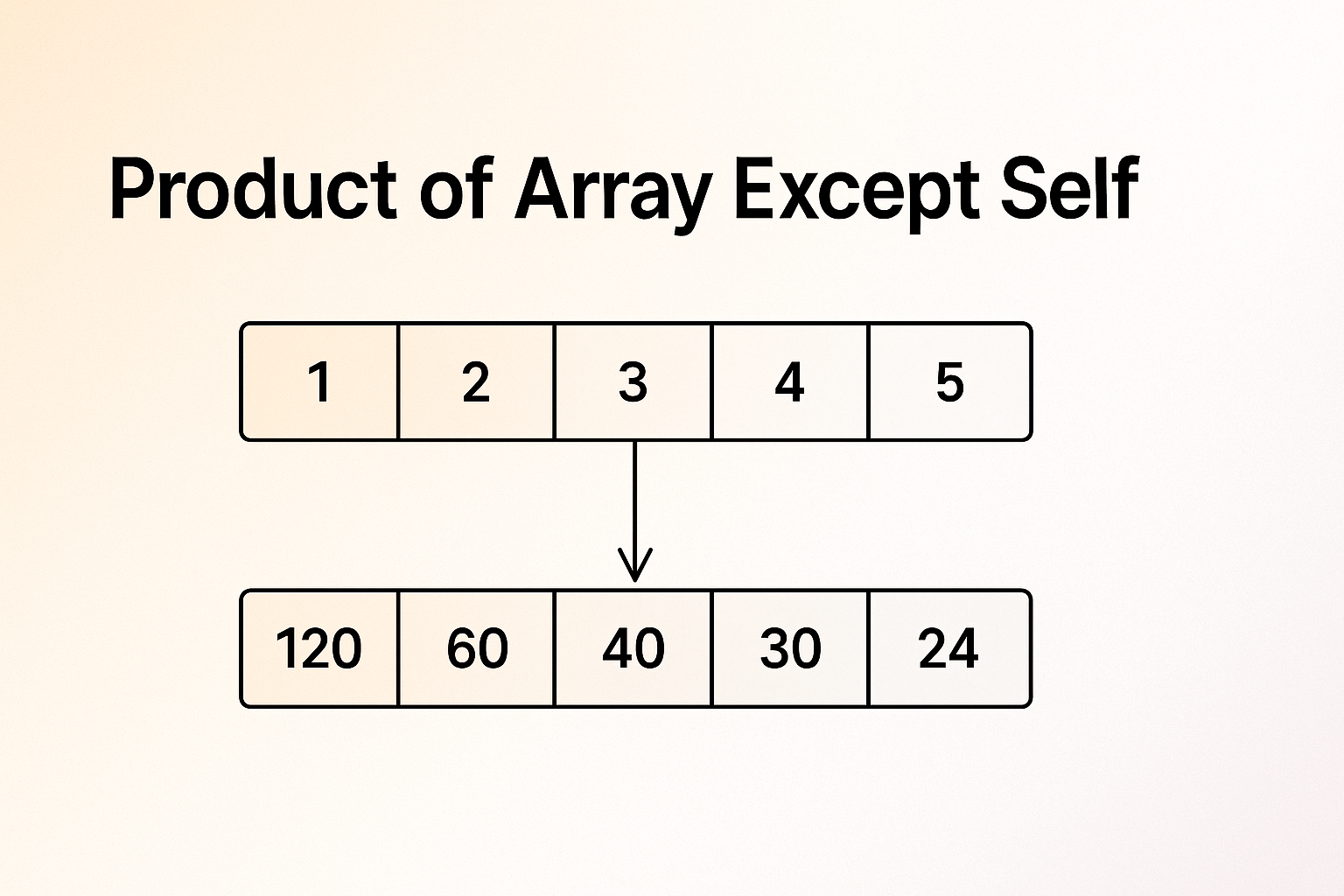
Given an array nums of n integers, create a new array result such that result[i] contains the product of all elements in nums except nums[i].
You must solve this problem without using the division operation and in O(n) time complexity.
For example:
- Input: nums = [1, 2, 3, 4]
- Output: result = [24, 12, 8, 6]
Here, result[0] = 2*3*4 = 24, result[1] = 1*3*4 = 12, and so on.
Brute Force Approach
Explanation
The most straightforward way to solve this problem is to use a nested loop:
- For each position i in the result array
- Calculate the product of all elements in the input array except the one at position i
This gives us the correct answer but requires O(n²) time complexity, which is not optimal for large arrays.
Calculating result[0]: 1 × 2 × 3 × 4 = 2 × 3 × 4 = 24
Calculating result[1]: 1 × 2 × 3 × 4 = 1 × 3 × 4 = 12
Calculating result[2]: 1 × 2 × 3 × 4 = 1 × 2 × 4 = 8
Calculating result[3]: 1 × 2 × 3 × 4 = 1 × 2 × 3 = 6
Result array: [24 , 12 , 8 ,6]
Code (Python)
def productExceptSelf(nums):
n = len(nums)
result = [1] * n
# For each position in the array
for i in range(n):
# Calculate product of all elements except nums[i]
for j in range(n):
if i != j: # Skip the current element
result[i] *= nums[j]
return resultCode (C++)
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> result(n, 1);
// For each position in the array
for (int i = 0; i < n; i++) {
// Calculate product of all elements except nums[i]
for (int j = 0; j < n; j++) {
if (i != j) { // Skip the current element
result[i] *= nums[j];
}
}
}
return result;
}Code (Java)
public static int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] result = new int[n];
// Initialize result array with 1's
Arrays.fill(result, 1);
// For each position in the array
for (int i = 0; i < n; i++) {
// Calculate product of all elements except nums[i]
for (int j = 0; j < n; j++) {
if (i != j) { // Skip the current element
result[i] *= nums[j];
}
}
}
return result
}
Optimized Approach
Explanation
The key insight for optimization is to use prefix and postfix products:
- Create an array result initialized with 1's
- First pass: Iterate from left to right, keeping track of the running product of all elements to the left of the current position
- Second pass: Iterate from right to left, keeping track of the running product of all elements to the right
- The final result at each position will be the product of its corresponding left and right products
This way, we calculate the products in O(n) time with just two passes through the array.
Consider the Example : [1 ,2 ,3 ,4]
This array basically tell the product of elements before it.
Now, with this array we iterate from right to left,Initialize the right product to 1.
result[3] = result[3] × right = 6 × 1 = 6
Update right = right × nums[3] = 1 × 4 = 4
result[2] = result[2] × right = 2 × 4 = 8
Update right = right × nums[2] = 4 × 3 = 12
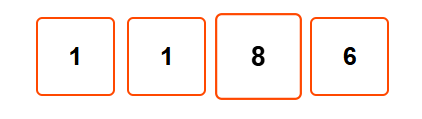
Repeating this process ,we get the final answer.
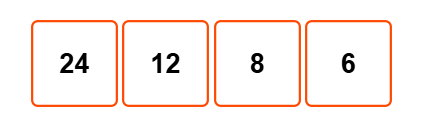
For each index, we've computed the product of all other elements:
result[0] = 2 × 3 × 4 = 24
result[1] = 1 × 3 × 4 = 12
result[2] = 1 × 2 × 4 = 8
result[3] = 1 × 2 × 3 = 6
Product of Array Except Self Visualization
<visualization-box>
Code (Python)
def productExceptSelf(nums):
n = len(nums)
result = [1] * n
# First pass: calculate products of all elements to the left
left_product = 1
for i in range(n):
result[i] = left_product # Store product of all elements to the left
left_product *= nums[i] # Update left product for next iteration
# Second pass: multiply by products of all elements to the right
right_product = 1
for i in range(n-1, -1, -1):
result[i] *= right_product # Multiply by product of all elements to the right
right_product *= nums[i] # Update right product for next iteration
return resultCode (C++)
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> result(n, 1);
// First pass: calculate products of all elements to the left
int left_product = 1;
for (int i = 0; i < n; i++) {
result[i] = left_product; // Store product of all elements to the left
left_product *= nums[i]; // Update left product for next iteration
}
// Second pass: multiply by products of all elements to the right
int right_product = 1;
for (int i = n - 1; i >= 0; i--) {
result[i] *= right_product; // Multiply by product of all elements to the right
right_product *= nums[i]; // Update right product for next iteration
}
return result;
}
Code (Java)
public static int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] result = new int[n];
int leftProduct = 1;
for (int i = 0; i < n; i++) {
result[i] = leftProduct;
leftProduct *= nums[i];
}
int rightProduct = 1;
for (int i = n - 1; i >= 0; i--) {
result[i] *= rightProduct;
rightProduct *= nums[i];
}
return result;
}
Conclusion
This problem is a classic example of how to use prefix and suffix arrays.
This idea can be further extended to finding maximum or minimum in the array except itself, and similar variations.
Key takeaways:
• Prefix/suffix computations are powerful techniques for array problems
• Make sure to use proper data types, else that would result in an overflow
