Find Longest Binary Subarray With Equal 0s and 1s | Tutorial
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
Problem Statement
Given a binary array consisting of 0s and 1s, find the length of the longest subarray that contains an equal number of 0s and 1s.
Example 1:
Input: [0, 1, 0, 1, 1, 0, 0]
Output: 6
Explanation: The subarray [0, 1, 0, 1, 1, 0] has 3 zeros and 3 ones.
Example 2:
Input: [1, 1, 1, 1, 0, 0]
Output: 4
Explanation: The subarray [1, 1, 0, 0] has 2 zeros and 2 ones.
Brute Force Approach
Explanation
The brute force approach is straightforward: we check every possible subarray to find the longest one with an equal count of 0s and 1s.
Here's how it works:
- Consider all possible subarrays by using two nested loops.
- For each subarray, count the number of 0s and 1s.
- If the counts are equal, update the maximum length if the current subarray is longer.
This approach is simple to implement but not efficient for large arrays.
Time Complexity: O(n³) where n is the length of the array.
- We have n² possible subarrays.
- For each subarray, we spend O(n) time counting 0s and 1s.
Space Complexity: O(1) as we only use a few variables.
Consider An Example array of [0 1 0 1 1 0]
We begin from index 0 and explore all subarrays starting from here.
- zeros = 0, ones = 0
Inner Loop: end = 0 → subarray = [0]
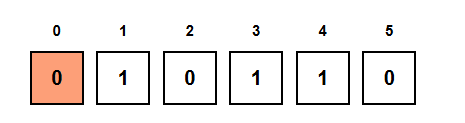
- We see a 0 → zeros = 1
- Not equal → skip
Inner Loop: end = 1 → subarray = [0, 1]
- We see a 1 → ones = 1
- zeros = 1, ones = 1 → Equal!
- Update max_length = max(0, 1 - 0 + 1) = 2
Inner Loop: end = 2 → subarray = [0, 1, 0]
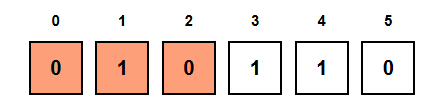
- We see a 0 → zeros = 2
- zeros = 2, ones = 1 → Not equal
Inner Loop: end = 3 → subarray = [0, 1, 0, 1]
- We see a 1 → ones = 2
- zeros = 2, ones = 2 → Equal!
- Update max_length = max(2, 3 - 0 + 1) = 4
Inner Loop: end = 4 → subarray = [0, 1, 0, 1, 1]
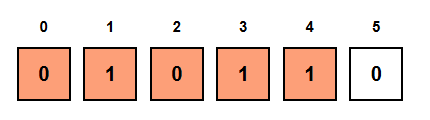
- We see a 1 → ones = 3
- zeros = 2, ones = 3 → Not equal
Inner Loop: end = 5 → subarray = [0, 1, 0, 1, 1, 0]
- We see a 0 → zeros = 3
- zeros = 3, ones = 3 → Equal!
- Update max_length = max(4, 5 - 0 + 1) = 6
Now start index will move to index 1 and the process repeats until start is less than 6.
Code (Python)
def find_max_length_brute_force(nums):
max_length = 0
n = len(nums)
# Check all possible subarrays
for start in range(n):
# Initialize counts for each new starting point
zeros = 0
ones = 0
for end in range(start, n):
# Count zeros and ones in current subarray
if nums[end] == 0:
zeros += 1
else:
ones += 1
# If equal number of zeros and ones, update max_length
if zeros == ones:
max_length = max(max_length, end - start + 1)
return max_length
Code (C++)
#include <vector>
#include <algorithm>
int findMaxLength_bruteForce(std::vector<int>& nums) {
int max_length = 0;
int n = nums.size();
// Check all possible subarrays
for (int start = 0; start < n; start++) {
// Initialize counts for each new starting point
int zeros = 0;
int ones = 0;
for (int end = start; end < n; end++) {
// Count zeros and ones in current subarray
if (nums[end] == 0) {
zeros++;
} else {
ones++;
}
// If equal number of zeros and ones, update max_length
if (zeros == ones) {
max_length = std::max(max_length, end - start + 1);
}
}
}
return max_length;
}
Code (Java)
class Solution {
public int findMaxLength_bruteForce(int[] nums) {
int maxLength = 0;
int n = nums.length;
// Check all possible subarrays
for (int start = 0; start < n; start++) {
// Initialize counts for each new starting point
int zeros = 0;
int ones = 0;
for (int end = start; end < n; end++) {
// Count zeros and ones in current subarray
if (nums[end] == 0) {
zeros++;
} else {
ones++;
}
// If equal number of zeros and ones, update maxLength
if (zeros == ones) {
maxLength = Math.max(maxLength, end - start + 1);
}
}
}
return maxLength;
}
}
Optimized Approach
Explanation
We can optimize this problem dramatically by using a clever trick: treat 0s as -1 and compute a running sum. When the sum becomes 0, we have an equal number of 0s and 1s.
The key insight is to use a hash map to track the first occurrence of each running sum. If we encounter the same sum again, it means the subarray between these two points has an equal number of 0s and 1s.
Here's how it works:
- Replace each 0 with -1 (conceptually).
- Calculate a running sum.
- Use a hash map to store the first index where each sum value occurred.
- When we see a sum that has occurred before, we calculate the length of the subarray.
- Keep track of the maximum length found.
Time Complexity: O(n) where n is the length of the array.
- We only need to traverse the array once.
Space Complexity: O(n) for the hash map.
Again let’s Consider the example [0, 1, 0, 1, 1, 0,0]
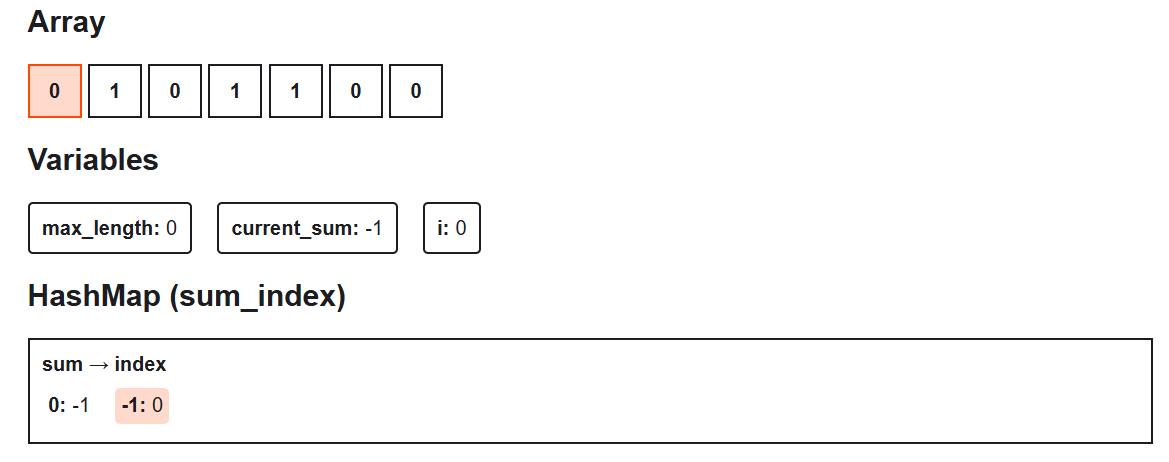
Step 1: i = 0, nums[0] = 0
- Treat 0 as -1 → current_sum = -1
- 1 not in sum_index → store sum_index[-1] = 0
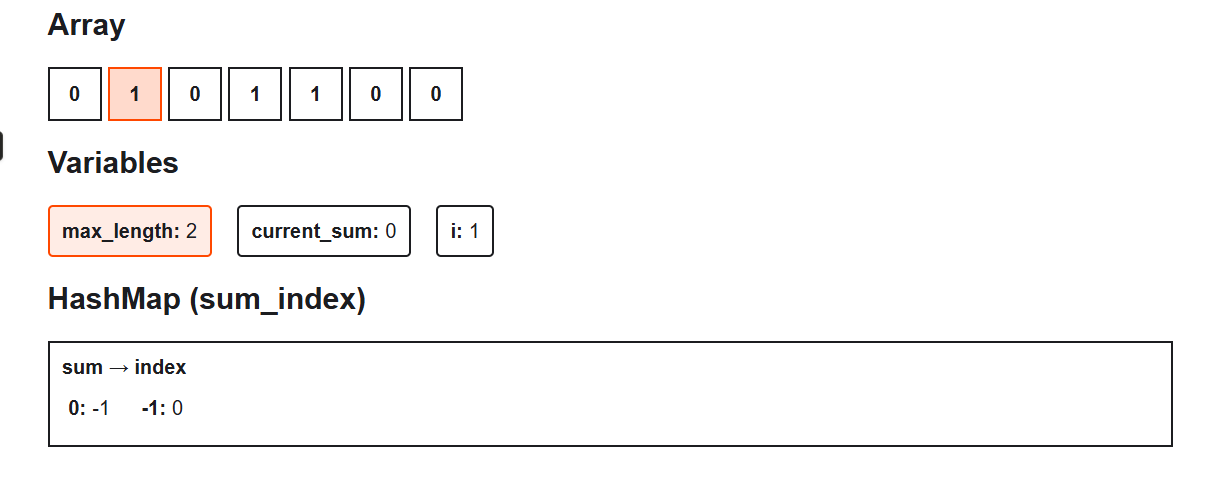
Step 2: i = 1, nums[1] = 1
- Add 1 → current_sum = 0
- 0 is in sum_index → subarray found from index 0 to 1
- Length = 1 - (-1) = 2 → max_length = 2
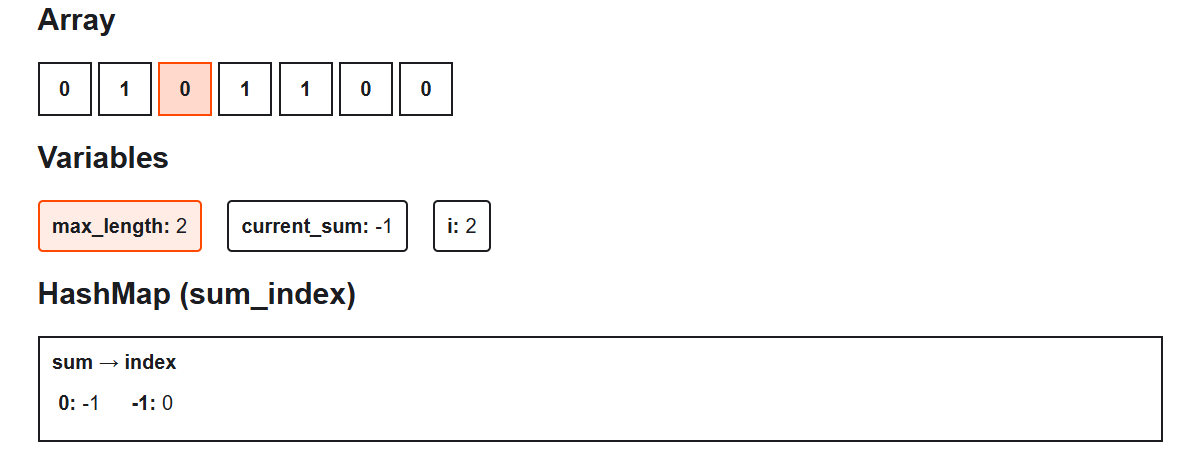
Step 3: i = 2, nums[2] = 0
- Add -1 → current_sum = -1
- 1 is in sum_index (first seen at index 0)
- Subarray from index 1 to 2 → length = 2 - 0 = 2 → max_length = 2 (no change)
Step 4: i = 3, nums[3] = 1
- Add 1 → current_sum = 0
- 0 is in sum_index (at index -1)
- Subarray from index 0 to 3 → length = 3 - (-1) = 4 → update max_length = 4
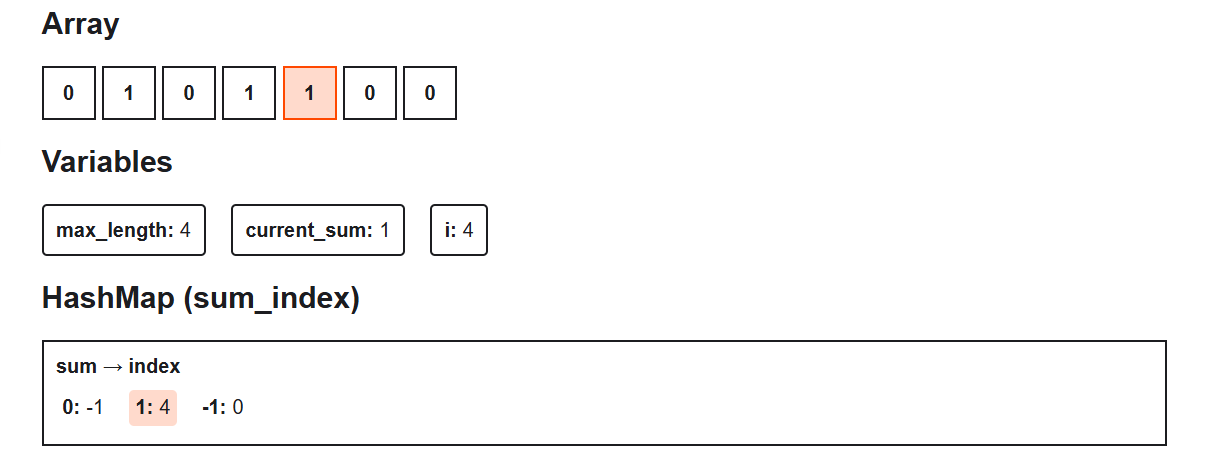
Step 5: i = 4, nums[4] = 1
- Add 1 → current_sum = 1
- 1 not in sum_index → store sum_index[1] = 4
Step 6: i = 5, nums[5] = 0
- Add -1 → current_sum = 0
- 0 is in sum_index (at index -1)
- Subarray from index 0 to 5 → length = 5 - (-1) = 6 → update max_length = 6
<visualization-box>
Code (Python)
def find_max_length(nums):
# HashMap to store the first occurrence of each sum
sum_index = {0: -1} # Initialize with sum 0 at index -1
max_length = 0
current_sum = 0
for i in range(len(nums)):
# Treat 0 as -1
current_sum += 1 if nums[i] == 1 else -1
# If current_sum seen before, we found a subarray with equal 0s and 1s
if current_sum in sum_index:
max_length = max(max_length, i - sum_index[current_sum])
else:
# Store first occurrence of this sum
sum_index[current_sum] = i
return max_length
Code (C++)
int findMaxLength(std::vector<int>& nums) {
// HashMap to store the first occurrence of each sum
std::unordered_map<int, int> sumIndex;
sumIndex[0] = -1; // Initialize with sum 0 at index -1
int maxLength = 0;
int currentSum = 0;
for (int i = 0; i < nums.size(); i++) {
// Treat 0 as -1
currentSum += (nums[i] == 1) ? 1 : -1;
// If currentSum seen before, we found a subarray with equal 0s and 1s
if (sumIndex.find(currentSum) != sumIndex.end()) {
maxLength = std::max(maxLength, i - sumIndex[currentSum]);
} else {
// Store first occurrence of this sum
sumIndex[currentSum] = i;
}
}
return maxLength;
}
Code (Java)
class Solution {
public int findMaxLength(int[] nums) {
// HashMap to store the first occurrence of each sum
Map<Integer, Integer> sumIndex = new HashMap<>();
sumIndex.put(0, -1); // Initialize with sum 0 at index -1
int maxLength = 0;
int currentSum = 0;
for (int i = 0; i < nums.length; i++) {
// Treat 0 as -1
currentSum += (nums[i] == 1) ? 1 : -1;
// If currentSum seen before, we found a subarray with equal 0s and 1s
if (sumIndex.containsKey(currentSum)) {
maxLength = Math.max(maxLength, i - sumIndex.get(currentSum));
} else {
// Store first occurrence of this sum
sumIndex.put(currentSum, i);
}
}
return maxLength;
}
}
Conclusion
The "Longest Subarray with Equal 0s and 1s" problem shows how a simple mathematical trick can transform a complex problem into a more manageable one. By converting 0s to -1s and tracking running sums, we reduced the time complexity from O(n³) to O(n).
Next time you face a similar problem about finding subarrays with certain properties, consider if you can transform the elements or use a running sum to simplify your solution.
