Linear Search Algorithm (Codes with Visualization)
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
Problem Statement
Linear search is defined as follows: Given an array of elements and a target value, find the index of the target value in the array. If the target value is not present in the array, return -1 or an appropriate indicator of absence.
For example, if we have the array [5, 2, 9, 1, 7] and we're searching for the value 9, the algorithm should return the index 2 (0-indexed).
Approach 1
Explanation
The approach 1 for linear search is quite intuitive: we check each element in the array one by one until we find the target value. If we reach the end of the array without finding the target, we conclude that it's not present.
This approach has a time complexity of O(n), where n is the number of elements in the array. In the worst case, we might need to check every element (if the target is at the end or not present at all).
The space complexity is O(1) since we only use a constant amount of extra space regardless of the input size.
Lets consider the array [5,2,9,1,7] and lets say our target value is 9.
Check index 0
Value = 5
5 != 9 → Not a match
Move to the next index
Step 1:
- Check index 0
- Value = 5
- 5 != 9 → Not a match
- Move to the next index
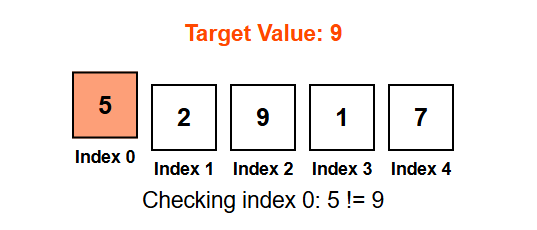
Step 2:
- Check index 1
- Value = 2
- 2 != 9 → Not a match
- Move to the next index
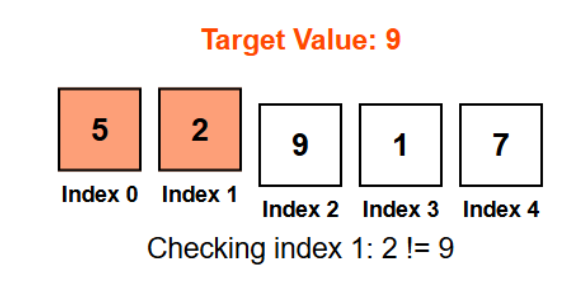
Step 3:
- Check index 2
- Value = 9
- 9 == 9 → Match found!
- Output: Found 9 at index 2
Code (Python)
def linear_search(arr, target):
"""
Perform a linear search to find the target in the array.
Parameters:
arr (list): The input array
target: The value to search for
Returns:
int: The index of the target if found, -1 otherwise
"""
# Iterate through each element in the array
for i in range(len(arr)):
# Check if the current element matches the target
if arr[i] == target:
return i # Return the index if found
# Return -1 if the target is not found
return -1
# Example usage
arr = [5, 2, 9, 1, 7]
target = 9
result = linear_search(arr, target)
print(f"Target {target} found at index: {result}")Code (C++)
#include <iostream>
#include <vector>
/**
* Perform a linear search to find the target in the array.
*
* @param arr The input array
* @param target The value to search for
* @return The index of the target if found, -1 otherwise
*/
int linearSearch(const std::vector<int>& arr, int target) {
// Iterate through each element in the array
for (int i = 0; i < arr.size(); i++) {
// Check if the current element matches the target
if (arr[i] == target) {
return i; // Return the index if found
}
}
// Return -1 if the target is not found
return -1;
}
int main() {
std::vector<int> arr = {5, 2, 9, 1, 7};
int target = 9;
int result = linearSearch(arr, target);
if (result != -1) {
std::cout << "Target " << target << " found at index: " << result << std::endl;
} else {
std::cout << "Target " << target << " not found in the array." << std::endl;
}
return 0;
}
Code (Java)
/**
* Linear search implementation
*/
public class LinearSearch {
/**
* Perform a linear search to find the target in the array.
*
* @param arr The input array
* @param target The value to search for
* @return The index of the target if found, -1 otherwise
*/
public static int linearSearch(int[] arr, int target) {
// Iterate through each element in the array
for (int i = 0; i < arr.length; i++) {
// Check if the current element matches the target
if (arr[i] == target) {
return i; // Return the index if found
}
}
// Return -1 if the target is not found
return -1;
}
public static void main(String[] args) {
int[] arr = {5, 2, 9, 1, 7};
int target = 9;
int result = linearSearch(arr, target);
if (result != -1) {
System.out.println("Target " + target + " found at index: " + result);
} else {
System.out.println("Target " + target + " not found in the array.");
}
}
}
Approach 2
Explanation
While linear search is already simple, there are a few optimizations we can consider:
- Early termination: If we know the array is sorted, we can stop searching once we find an element greater than our target.
- Two-pointer technique: We can search from both ends of the array simultaneously, potentially reducing the number of comparisons by half.
- Sentinel approach: We can add the target value at the end of the array as a sentinel, which eliminates the need to check the loop condition on each iteration.
Let's implement the two-pointer technique as it's a good balance of simplicity and efficiency.
With this optimization, the worst-case time complexity remains O(n), but on average, we might find the target in about half the time compared to the brute force approach. The space complexity is still O(1).
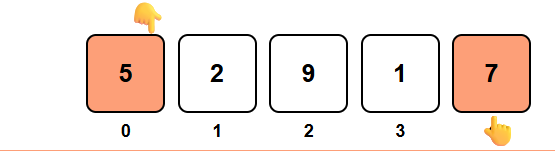
Step 1: Checked indices 0 and 4, target not found. Moving pointers inward.
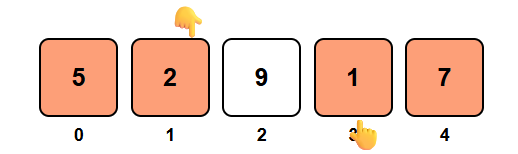
Step 2: Checked indices 1 and 3, target not found. Moving pointers inward.
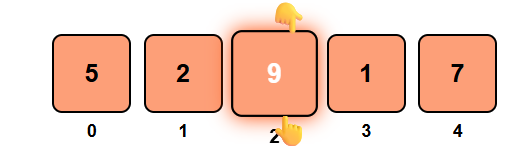
Step 3: Found target 9 at left pointer position (index 2)!
Linear Search Algorithm Visualization
<visualization-box>
Code (Python)
def optimized_linear_search(arr, target):
"""
Perform an optimized linear search using the two-pointer technique.
Parameters:
arr (list): The input array
target: The value to search for
Returns:
int: The index of the target if found, -1 otherwise
"""
left = 0
right = len(arr) - 1
# Search from both ends of the array
while left <= right:
# Check if target is at the left pointer
if arr[left] == target:
return left
# Check if target is at the right pointer
if arr[right] == target:
return right
# Move both pointers inward
left += 1
right -= 1
# Return -1 if the target is not found
return -1
# Example usage
arr = [5, 2, 9, 1, 7]
target = 9
result = optimized_linear_search(arr, target)
print(f"Target {target} found at index: {result}")Code (C++)
#include <iostream>
#include <vector>
/**
* Perform an optimized linear search using the two-pointer technique.
*
* @param arr The input array
* @param target The value to search for
* @return The index of the target if found, -1 otherwise
*/
int optimizedLinearSearch(const std::vector<int>& arr, int target) {
int left = 0;
int right = arr.size() - 1;
// Search from both ends of the array
while (left <= right) {
// Check if target is at the left pointer
if (arr[left] == target) {
return left;
}
// Check if target is at the right pointer
if (arr[right] == target) {
return right;
}
// Move both pointers inward
left++;
right--;
}
// Return -1 if the target is not found
return -1;
}
int main() {
std::vector<int> arr = {5, 2, 9, 1, 7};
int target = 9;
int result = optimizedLinearSearch(arr, target);
if (result != -1) {
std::cout << "Target " << target << " found at index: " << result << std::endl;
} else {
std::cout << "Target " << target << " not found in the array." << std::endl;
}
return 0;
}
Code (Java)
/**
* Optimized linear search implementation
*/
public class OptimizedLinearSearch {
/**
* Perform an optimized linear search using the two-pointer technique.
*
* @param arr The input array
* @param target The value to search for
* @return The index of the target if found, -1 otherwise
*/
public static int optimizedLinearSearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
// Search from both ends of the array
while (left <= right) {
// Check if target is at the left pointer
if (arr[left] == target) {
return left;
}
// Check if target is at the right pointer
if (arr[right] == target) {
return right;
}
// Move both pointers inward
left++;
right--;
}
// Return -1 if the target is not found
return -1;
}
public static void main(String[] args) {
int[] arr = {5, 2, 9, 1, 7};
int target = 9;
int result = optimizedLinearSearch(arr, target);
if (result != -1) {
System.out.println("Target " + target + " found at index: " + result);
} else {
System.out.println("Target " + target + " not found in the array.");
}
}
}
Conclusion
Linear search is a simple yet essential algorithm that serves as a building block for more complex searching techniques. While it may not be the most efficient for large datasets (compared to binary search on sorted arrays, for example), it's perfectly suitable for small arrays or unsorted data.
The brute force approach checks each element sequentially, while our optimized version uses the two-pointer technique to potentially reduce the number of comparisons. Both versions maintain a time complexity of O(n) in the worst case, but the optimized version can perform better on average.
Learning to improve basic algorithms like linear search helps develop important programming skills and a deeper appreciation for algorithm efficiency. These principles can be applied to more complex problems as you continue your programming journey.
