Leaders in an Array: Solutions with Code and Visualization
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
Problem Statement
In an array, a "leader" is an element that is greater than all elements to its right. The rightmost element is always a leader (since there are no elements to its right).
For example, in the array [16, 17, 4, 3, 5, 2], the leaders are 17, 5, and 2.
Your task is to write a function that identifies all the leaders in a given array.
Brute Force Approach
Explanation
The most straightforward way to solve this problem is to use a nested loop approach:
- For each element in the array, check if it's greater than ALL elements to its right
- If yes, it's a leader
This approach is intuitive but not efficient for large arrays.
Code (Python)
def find_leaders_brute_force(arr):
n = len(arr)
leaders = []
for i in range(n):
# Assume current element is a leader
is_leader = True
# Check if any element to the right is greater
for j in range(i+1, n):
if arr[i] <= arr[j]:
is_leader = False
break
# If no greater element found to the right, it's a leader
if is_leader:
leaders.append(arr[i])
return leaders
# Example usage
arr = [16, 17, 4, 3, 5, 2]
print(find_leaders_brute_force(arr)) # Output: [17, 5, 2]Code (C++)
#include <iostream>
#include <vector>
using namespace std;
vector<int> findLeadersBruteForce(vector<int> arr) {
int n = arr.size();
vector<int> leaders;
for (int i = 0; i < n; i++) {
// Assume current element is a leader
bool isLeader = true;
// Check if any element to the right is greater
for (int j = i + 1; j < n; j++) {
if (arr[i] <= arr[j]) {
isLeader = false;
break;
}
}
// If no greater element found to the right, it's a leader
if (isLeader) {
leaders.push_back(arr[i]);
}
}
return leaders;
}
// Example usage
int main() {
vector<int> arr = {16, 17, 4, 3, 5, 2};
vector<int> result = findLeadersBruteForce(arr);
cout << "Leaders: ";
for (int leader : result) {
cout << leader << " ";
}
return 0;
}
Code (Java)
public class LeadersInArray {
public static List<Integer> findLeadersBruteForce(int[] arr) {
int n = arr.length;
List<Integer> leaders = new ArrayList<>();
for (int i = 0; i < n; i++) {
// Assume current element is a leader
boolean isLeader = true;
// Check if any element to the right is greater
for (int j = i + 1; j < n; j++) {
if (arr[i] <= arr[j]) {
isLeader = false;
break;
}
}
// If no greater element found to the right, it's a leader
if (isLeader) {
leaders.add(arr[i]);
}
}
return leaders;
}
public static void main(String[] args) {
int[] arr = {16, 17, 4, 3, 5, 2};
List<Integer> result = findLeadersBruteForce(arr);
System.out.print("Leaders: ");
for (int leader : result) {
System.out.print(leader + " ");
}
}
}
Time Complexity: O(n²) where n is the size of the array
Space Complexity: O(1) excluding the output array
Optimized Approach
Explanation
We can optimize this solution by scanning the array from right to left:
- Start from the rightmost element (which is always a leader)
- Keep track of the maximum element seen so far
- Any element greater than the current maximum is a leader
This approach is much more efficient as it requires only a single pass through the array.
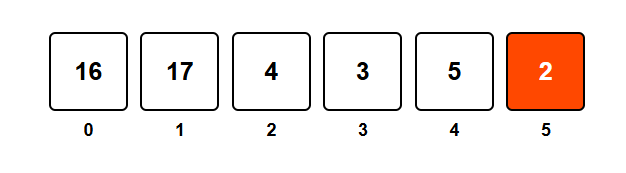
Let's start from the rightmost element. The last element (2) is always a leader since there are no elements to its right.
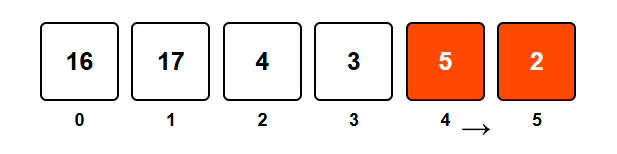
Now we move left. Is 5 greater than 2? Yes! So 5 is a leader.
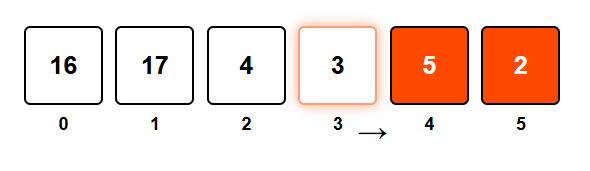
Next, is 3 greater than the maximum element to its right (which is 5)? No, 3 < 5, so 3 is not a leader.
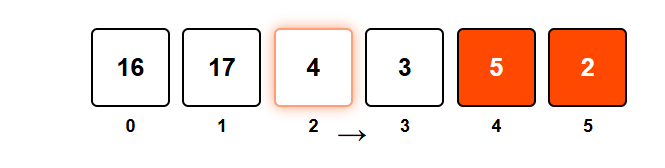
Next, is 4 greater than the maximum element to its right (which is 5)? No, 4 < 5, so 4 is not a leader.
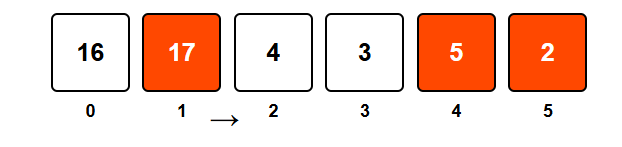
Now, is 17 greater than the maximum element to its right (which is 5)? Yes! So 17 is a leader.
Leaders in an Array Visualization
<visualization-box>
Code (Python)
def find_leaders(arr):
n = len(arr)
leaders = []
# The rightmost element is always a leader
max_right = arr[n-1]
leaders.append(max_right)
# Scan from right to left
for i in range(n-2, -1, -1):
if arr[i] > max_right:
# Update the maximum and add to leaders
max_right = arr[i]
leaders.append(max_right)
# The leaders are collected from right to left, so reverse
leaders.reverse()
return leaders
# Example usage
arr = [16, 17, 4, 3, 5, 2]
print(find_leaders(arr)) # Output: [17, 5, 2]Code (C++)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> findLeaders(vector<int> arr) {
int n = arr.size();
vector<int> leaders;
// The rightmost element is always a leader
int maxRight = arr[n-1];
leaders.push_back(maxRight);
// Scan from right to left
for (int i = n - 2; i >= 0; i--) {
if (arr[i] > maxRight) {
// Update the maximum and add to leaders
maxRight = arr[i];
leaders.push_back(maxRight);
}
}
// The leaders are collected from right to left, so reverse
reverse(leaders.begin(), leaders.end());
return leaders;
}
// Example usage
int main() {
vector<int> arr = {16, 17, 4, 3, 5, 2};
vector<int> result = findLeaders(arr);
cout << "Leaders: ";
for (int leader : result) {
cout << leader << " ";
}
return 0;
}
Code (Java)
import java.util.*;
public class LeadersInArray {
public static List<Integer> findLeaders(int[] arr) {
int n = arr.length;
List<Integer> leaders = new ArrayList<>();
// The rightmost element is always a leader
int maxRight = arr[n-1];
leaders.add(maxRight);
// Scan from right to left
for (int i = n - 2; i >= 0; i--) {
if (arr[i] > maxRight) {
// Update the maximum and add to leaders
maxRight = arr[i];
leaders.add(maxRight);
}
}
// The leaders are collected from right to left, so reverse
Collections.reverse(leaders);
return leaders;
}
public static void main(String[] args) {
int[] arr = {16, 17, 4, 3, 5, 2};
List<Integer> result = findLeaders(arr);
System.out.print("Leaders: ");
for (int leader : result) {
System.out.print(leader + " ");
}
}
}
Time Complexity: O(n) where n is the size of the array
Space Complexity: O(1) excluding the output array
Conclusion
The "Leaders in an Array" problem teaches us something very important that not every time we traverse left to right but sometimes it’s optimal if we do the reverse!
1. The brute force approach is straightforward but inefficient with O(n²) time complexity.
2. By thinking differently about the problem—scanning from right to left rather than left to right—we can create a much more efficient O(n) solution.
3. The optimized solution doesn't just reduce computational steps; it also simplifies the code.
