Kth Missing Positive Number: Codes with Visualization
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
Problem Statement
Given an array of positive integers sorted in strictly increasing order, and an integer k, we need to find the kth positive integer that is missing from this array.
For example:
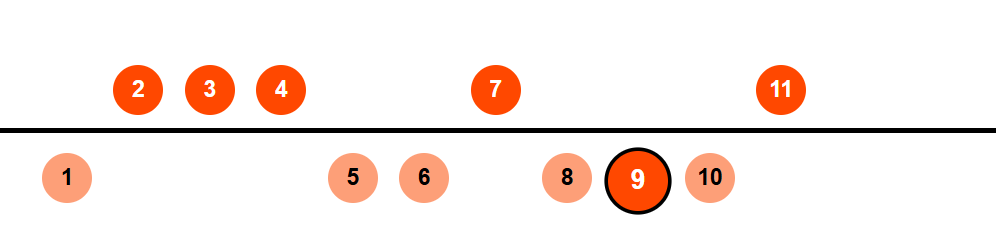
- If arr = [2, 3, 4, 7, 11] and k = 5, the missing positive integers are 1, 5, 6, 8, 9, 10, 12, 13, ... and the 5th missing positive integer is 9.
Brute Force Approach
Explanation
The simplest way to solve this problem is to check each positive integer, starting from 1, and see if it's in the array. We keep track of how many missing numbers we've found, and once we reach the kth missing number, we return it.
This approach is straightforward:
- Start counting from the first positive integer (1)
- For each number, check if it's in the array
- If it's not in the array, increment our count of missing numbers
- When we reach the kth missing number, return it
The time complexity is O(n + m) where n is the size of the input array and m is the value of the kth missing positive integer. This is because we might need to check positive integers up to the value of the answer.
Space complexity is O(1) as we only use a few variables regardless of input size.
Consider an array arr =[2, 3, 4, 7, 11] and k = 5, the missing positive integers are 1, 5, 6, 8, 9, 10, 12, 13, ... and the 5th missing positive integer is 9.
Code (Python)
def findKthPositive(arr, k):
# Start with the first positive integer
current_num = 1
# Counter for missing numbers found
missing_count = 0
# Continue until we find the kth missing number
while missing_count < k:
# Check if current_num is in arr
if current_num not in arr:
missing_count += 1
# If we found the kth missing number, return it
if missing_count == k:
return current_num
# Move to the next number
current_num += 1
return -1 # This line should never be reached with valid inputs
C++ Code
#include <vector>
using namespace std;
int findKthPositive(vector<int>& arr, int k) {
// Start with the first positive integer
int current_num = 1;
// Counter for missing numbers found
int missing_count = 0;
// Continue until we find the kth missing number
while (missing_count < k) {
// Flag to check if current_num is in arr
bool found = false;
// Check if current_num is in arr
for (int num : arr) {
if (num == current_num) {
found = true;
break;
}
}
// If current_num is not in arr, increment missing_count
if (!found) {
missing_count++;
// If we found the kth missing number, return it
if (missing_count == k) {
return current_num;
}
}
// Move to the next number
current_num++;
}
return -1; // This line should never be reached with valid inputs
}
Java Code
public class Solution {
public int findKthPositive(int[] arr, int k) {
// Start with the first positive integer
int currentNum = 1;
// Counter for missing numbers found
int missingCount = 0;
// Continue until we find the kth missing number
while (missingCount < k) {
// Flag to check if currentNum is in arr
boolean found = false;
// Check if currentNum is in arr
for (int num : arr) {
if (num == currentNum) {
found = true;
break;
}
}
// If currentNum is not in arr, increment missingCount
if (!found) {
missingCount++;
// If we found the kth missing number, return it
if (missingCount == k) {
return currentNum;
}
}
// Move to the next number
currentNum++;
}
return -1; // This line should never be reached with valid inputs
}
}
Optimized Approach
Explanation
The brute force approach works, but it's not efficient for large arrays or large values of k. We can optimize by using the sorted nature of the input array.
Here's the key insight: at any index i in the array, the number of positive integers missing up to arr[i] is (arr[i] - (i + 1)).
For example, in [2, 3, 4, 7, 11]:
- At index 0, arr[0] = 2, so (2 - (0 + 1)) = 1 number is missing (which is 1)
- At index 3, arr[3] = 7, so (7 - (3 + 1)) = 3 numbers are missing (which are 1, 5, 6)
We can use binary search to find the position where the kth missing number would be:
- Use binary search to find the index where the count of missing numbers becomes >= k
- Once we find this index, we can calculate the kth missing number
The time complexity is O(log n) where n is the size of the input array.
The space complexity remains O(1).
Consider [2, 3, 4, 7, 11] and k = 5, the missing positive integers are 1, 5, 6, 8, 9, 10, 12, 13, ... and the 5th missing positive integer is 9.
First Iteration
- mid = (0 + 4) // 2 = 2
- arr[mid] = 4
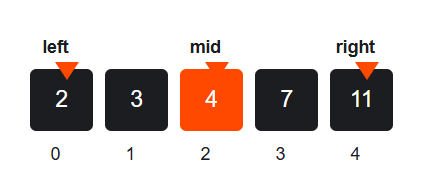
- missing_count = arr[mid] - (mid + 1) = 4 - 3 = 1
- Since 1 < 5, move search right:
→ left = mid + 1 = 3
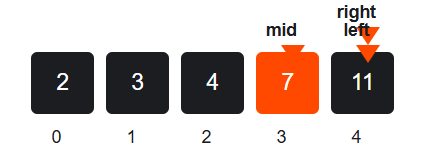
Second Iteration
- mid = (3 + 4) // 2 = 3
- arr[mid] = 7
- missing_count = 7 - (3 + 1) = 7 - 4 = 3
- Still 3 < 5, move search right:
→ left = mid + 1 = 4
Third Iteration
- mid = (4 + 4) // 2 = 4
- arr[mid] = 11
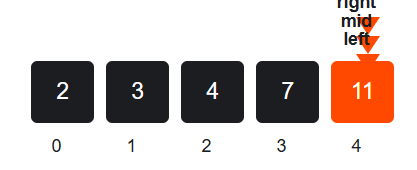
- missing_count = 11 - (4 + 1) = 11 - 5 = 6
- Now 6 >= 5, move left:
→ right = mid - 1 = 3
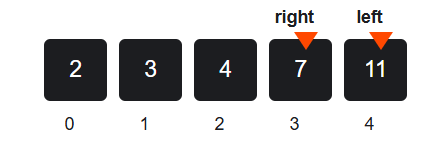
End of Loop
- Loop exits since left > right (left = 4, right = 3)
- Now apply the formula:
→ return k + right + 1 = 5 + 3 + 1 = 9
Final Answer: 9
So, the 5th missing positive number is 9.
Kth Missing Positive Number Visualization
<visualization-box>
Code (Python)
def findKthPositive(arr, k):
left, right = 0, len(arr) - 1
# Binary search to find the position where missing count >= k
while left <= right:
mid = (left + right) // 2
# Calculate number of missing integers up to arr[mid]
missing_count = arr[mid] - (mid + 1)
if missing_count < k:
left = mid + 1
else:
right = mid - 1
# At this point, 'right' is the last position with missing_count < k
# or -1 if all positions have missing_count >= k
# The kth missing number is k steps ahead of (right + 1)
return k + right + 1
Code (C++)
#include <vector>
using namespace std;
int findKthPositive(vector<int>& arr, int k) {
int left = 0;
int right = arr.size() - 1;
// Binary search to find the position where missing count >= k
while (left <= right) {
int mid = left + (right - left) / 2;
// Calculate number of missing integers up to arr[mid]
int missing_count = arr[mid] - (mid + 1);
if (missing_count < k) {
left = mid + 1;
} else {
right = mid - 1;
}
}
// At this point, 'right' is the last position with missing_count < k
// or -1 if all positions have missing_count >= k
// The kth missing number is k steps ahead of (right + 1)
return k + right + 1;
}
Code (Java)
public class Solution {
public int findKthPositive(int[] arr, int k) {
int left = 0;
int right = arr.length - 1;
// Binary search to find the position where missing count >= k
while (left <= right) {
int mid = left + (right - left) / 2;
// Calculate number of missing integers up to arr[mid]
int missingCount = arr[mid] - (mid + 1);
if (missingCount < k) {
left = mid + 1;
} else {
right = mid - 1;
}
}
// At this point, 'right' is the last position with missingCount < k
// or -1 if all positions have missingCount >= k
// The kth missing number is k steps ahead of (right + 1)
return k + right + 1;
}
}
Conclusion
The "Kth Missing Positive Number" problem teaches us how to efficiently find missing elements in a sorted array. We explored two approaches:
1. A brute force method that checks each positive integer one by one, with O(n + m) time complexity.
2. An optimized solution using binary search that reduces the time complexity to O(log n).
This problem shows how important it is to analyze the properties of the input data (like the sorted nature of the array) to create more efficient algorithms.
