Count Inversions of an Array: Codes with Visualization
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
Problem Statement
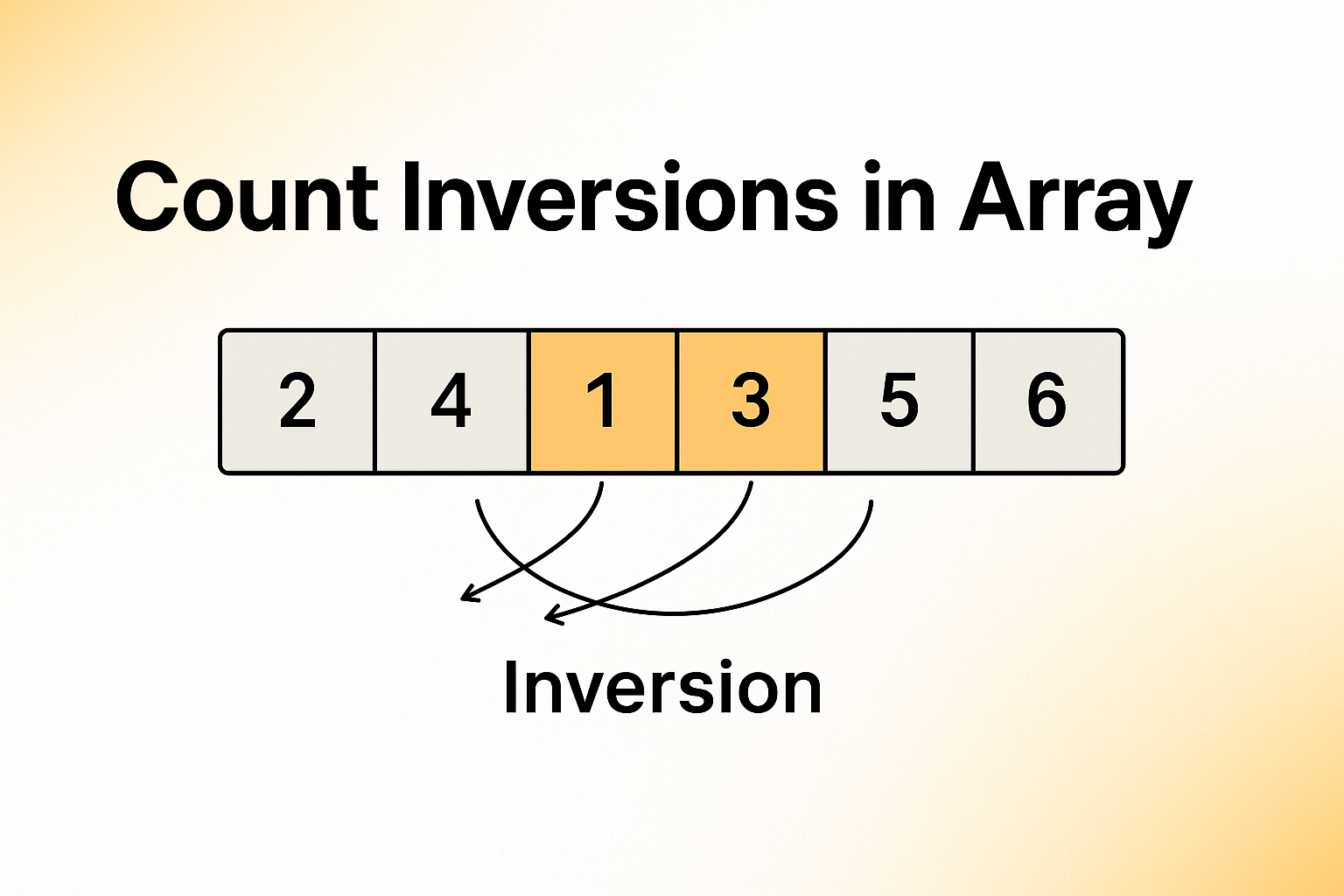
Given an array of integers, count the number of inversions in the array.
An inversion occurs when two elements in the array are out of their natural order. Formally, two elements A[i] and A[j] form an inversion if A[i] > A[j] and i < j.
For example, in the array [2, 4, 1, 3, 5]:
(2, 1) is an inversion because 2 > 1 and 2 appears before 1
(4, 1) is an inversion because 4 > 1 and 4 appears before 1
(4, 3) is an inversion because 4 > 3 and 4 appears before 3
So this array has 3 inversions in total.
Brute Force Approach
Explanation
The most straightforward way to solve this problem is to check every possible pair of elements in the array. For each element, we compare it with all elements that come after it. If the current element is greater than any of the following elements, we count it as an inversion.
This approach requires two nested loops:
- The outer loop iterates through each element in the array
- The inner loop checks all elements that come after the current element
While this solution is easy to implement, it has a time complexity of O(n²), which becomes inefficient for large arrays.
Code (Python)
def count_inversions_brute_force(arr):
n = len(arr)
inversion_count = 0
# Check each pair of elements
for i in range(n):
for j in range(i+1, n):
# If elements are out of order, count an inversion
if arr[i] > arr[j]:
inversion_count += 1
return inversion_countCode (C++)
int countInversionsBruteForce(const std::vector<int>& arr) {
int n = arr.size();
int inversionCount = 0;
// Check each pair of elements
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// If elements are out of order, count an inversion
if (arr[i] > arr[j]) {
inversionCount++;
}
}
}
return inversionCount;
}Code (Java)
public static int countInversionsBruteForce(int[] arr) {
int n = arr.length;
int inversionCount = 0;
// Check each pair of elements
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// If elements are out of order, count an inversion
if (arr[i] > arr[j]) {
inversionCount++;
}
}
}
return inversionCount;
}Optimized Approach
Explanation
We can optimize our solution using a modified merge sort algorithm. The key insight is that inversions correspond to the number of elements that need to be swapped to sort the array.
During the merge step of merge sort, when we pick an element from the right subarray before an element from the left subarray, that's exactly when an inversion occurs. By counting these occurrences during the merge process, we can count all inversions.
Here's how it works:
- Split the array into two halves recursively
- Count inversions in the left half
- Count inversions in the right half
- Count split inversions (inversions across the two halves) while merging
- Return the sum of all three counts
This approach has a time complexity of O(n log n), much better than the brute force O(n²).
Let's Take a look How exactly the inversion are being counted in the merge step.
Let's say we want to merge [2 , 4] and [1 , 3, 4]
At its core, merge sort relies on the idea that the right-side elements should be greater than the left-side elements in a sorted array. When this natural order is violated, we detect an inversion — a scenario where a smaller element appears after a larger one.
Now, during the merge step, both halves are already sorted. So when we compare elements from the left and right subarrays:
- If the element from the left is smaller, everything is fine — no inversion.
- But if the element from the right is smaller than the left, then we’ve found more than just one inversion.
Why? Because the right element is smaller than all the remaining elements in the left half (since the left half is sorted).
So this one element from the right forms an inversion pair with every unmerged element in the left half.
That’s the key optimization — instead of checking each pair individually, we can count all these inversions in one go as:
inversions += (number of remaining elements in left half)
Lets Dry Run:
Initial:
- i = 0 → Left[i] = 2
- j = 0 → Right[j] = 1
Compare 2 and 1:
Since 2 > 1, this is an inversion.
And not just one inversion:
All remaining elements in Left from index i onwards will also be greater than 1.
So count len(Left) - i = 2 inversions.
Add 1 to the merged array, move j to 1.
Inversions so far: 2
Now:
- i = 0 → Left[i] = 2
- j = 1 → Right[j] = 3
2 < 3 → No inversion.
Add 2 to merged array, move i to 1.
Now:
- i = 1 → Left[i] = 4
- j = 1 → Right[j] = 3
4 > 3 → Inversion.
Remaining elements in Left from index 1 onwards = 1 → So 1 inversion.
Add 3 to merged array, move j to 2.
Inversions so far: 2 + 1 = 3
Now:
- i = 1 → Left[i] = 4
- j = 2 → Right[j] = 4
4 <= 4 → No inversion.
Add 4 to merged array, move i to 2.
Now since the left is exhausted we will just remaining elements from the right array.
Count Inversions in Array Visualization
<visualization-box>
Code (Python)
def merge_sort_and_count(arr):
# Returns a tuple: (sorted_array, inversion_count)
if len(arr) <= 1:
return arr, 0
# Split the array into two halves
mid = len(arr) // 2
left, inv_left = merge_sort_and_count(arr[:mid])
right, inv_right = merge_sort_and_count(arr[mid:])
# Merge the two halves and count split inversions
merged, split_inv = merge_and_count_split_inv(left, right)
# Total inversions = inversions in left + inversions in right + split inversions
return merged, inv_left + inv_right + split_inv
def merge_and_count_split_inv(left, right):
merged = []
inv_count = 0
i = j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
merged.append(left[i])
i += 1
else:
# This is where inversions are counted!
# When right[j] is placed before the remaining elements in left,
# each remaining element in left forms an inversion with right[j]
merged.append(right[j])
inv_count += len(left) - i
j += 1
# Add remaining elements
merged.extend(left[i:])
merged.extend(right[j:])
return merged, inv_count
def count_inversions_optimized(arr):
_, inv_count = merge_sort_and_count(arr)
return inv_count
Code (C++)
// Merge function that also counts inversions
std::pair<std::vector<int>, long long> mergeAndCount(const std::vector<int>& left, const std::vector<int>& right) {
std::vector<int> merged;
long long invCount = 0;
int i = 0, j = 0;
while (i < left.size() && j < right.size()) {
if (left[i] <= right[j]) {
merged.push_back(left[i]);
i++;
} else {
// This is where inversions are counted!
merged.push_back(right[j]);
invCount += left.size() - i; // Count split inversions
j++;
}
}
// Add remaining elements
while (i < left.size()) {
merged.push_back(left[i]);
i++;
}
while (j < right.size()) {
merged.push_back(right[j]);
j++;
}
return {merged, invCount};
}
// Modified merge sort that counts inversions
std::pair<std::vector<int>, long long> mergeSortAndCount(std::vector<int> arr) {
if (arr.size() <= 1) {
return {arr, 0};
}
int mid = arr.size() / 2;
std::vector<int> left(arr.begin(), arr.begin() + mid);
std::vector<int> right(arr.begin() + mid, arr.end());
// Recursively count inversions in left and right subarrays
auto [sortedLeft, invLeft] = mergeSortAndCount(left);
auto [sortedRight, invRight] = mergeSortAndCount(right);
// Count split inversions and merge
auto [merged, splitInv] = mergeAndCount(sortedLeft, sortedRight);
return {merged, invLeft + invRight + splitInv};
}
long long countInversionsOptimized(std::vector<int> arr) {
auto [_, invCount] = mergeSortAndCount(arr);
return invCount;
}
Code (Java)
public static long countInversionsOptimized(int[] arr) {
return mergeSortAndCount(arr, 0, arr.length - 1);
}
// Modified merge sort that counts inversions
private static long mergeSortAndCount(int[] arr, int left, int right) {
long invCount = 0;
if (left < right) {
int mid = (left + right) / 2;
// Count inversions in left subarray
invCount += mergeSortAndCount(arr, left, mid);
// Count inversions in right subarray
invCount += mergeSortAndCount(arr, mid + 1, right);
// Count split inversions during merge
invCount += mergeAndCountSplitInv(arr, left, mid, right);
}
return invCount;
}
// Merge function that also counts inversions
private static long mergeAndCountSplitInv(int[] arr, int left, int mid, int right) {
// Create temporary arrays for merging
int[] leftArray = Arrays.copyOfRange(arr, left, mid + 1);
int[] rightArray = Arrays.copyOfRange(arr, mid + 1, right + 1);
int i = 0, j = 0, k = left;
long invCount = 0;
while (i < leftArray.length && j < rightArray.length) {
if (leftArray[i] <= rightArray[j]) {
arr[k++] = leftArray[i++];
} else {
// This is where inversions are counted!
arr[k++] = rightArray[j++];
invCount += (leftArray.length - i); // Count split inversions
}
}
// Add remaining elements
while (i < leftArray.length) {
arr[k++] = leftArray[i++];
}
while (j < rightArray.length) {
arr[k++] = rightArray[j++];
}
return invCount;
}
Conclusion
We've explored two approaches to counting inversions in an array:
1. The brute force approach with O(n²) time complexity, which is simple but inefficient for large inputs
2. The optimized approach using merge sort with O(n log n) time complexity
The optimized solution demonstrates how a sorting algorithm can be modified to solve a different problem efficiently. This type of algorithmic thinking is valuable in solving many problems where the naive approach is too slow.
