Check Redundant Brackets in Expressions: Code Examples
Sasank is a Technical Content Writer with a strong background in competitive programming. He has solved nearly 1500 problems on LeetCode and achieved top rankings in LeetCode Weekly Contests, including global ranks of 171, 196, 206, 308, 352, and more. His expertise in algorithms and problem-solving is also reflected in his active participation on platforms like Codeforces. Sasank enjoys sharing his technical knowledge and helping others learn by creating clear and accessible content.
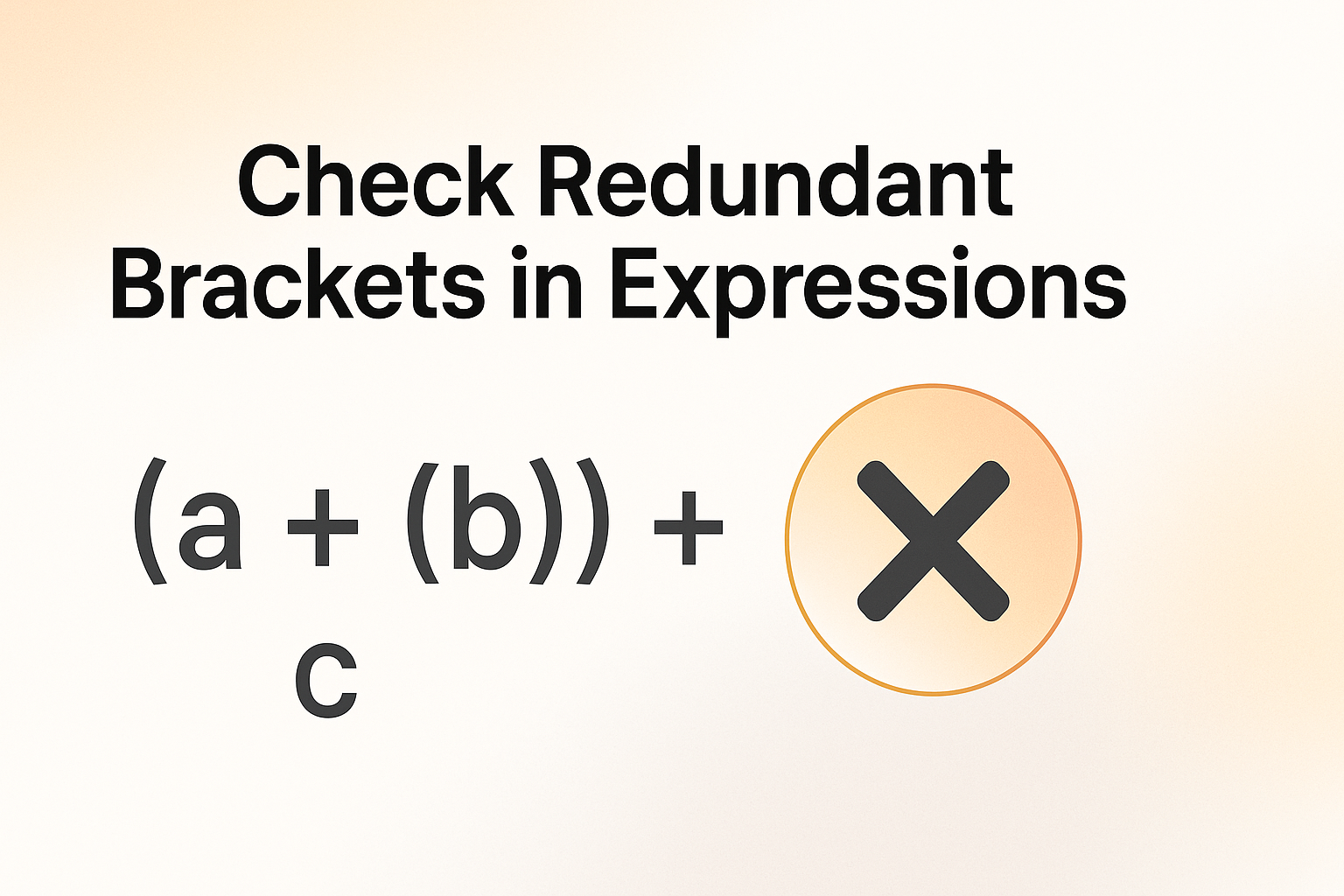
Problem Statement
Given a string containing a mathematical expression with parentheses, determine if it contains any redundant brackets. Redundant brackets are those that don't add any value to the expression - they can be removed without changing the meaning of the expression.
For example:
- ((a+b)) has redundant brackets because the outer pair doesn't change the evaluation order.
- (a+(b*c)) doesn't have redundant brackets as all brackets are necessary.
Brute Force Approach
Explanation
The simplest way to tackle this problem is to check each closing bracket we encounter. For every closing bracket, we can trace back to its matching opening bracket and check if the enclosed expression is just another bracketed expression or a single operand.
However, this approach becomes quite inefficient for complex expressions as we would need to repeatedly parse the same parts of the expression multiple times.
Time Complexity: O(n²) where n is the length of the expression
Space Complexity: O(1)
Code Implementation
Python
def check_redundant_brackets(expr):
# Function to check if a string has redundant brackets
for i in range(len(expr)):
if expr[i] == ')':
j = i - 1
has_operator = False
count = 0
# Move backward until matching '(' is found
while j >= 0 and expr[j] != '(':
if expr[j] in '+-*/':
has_operator = True
count += 1
j -= 1
# If no operator or empty brackets, it's redundant
if not has_operator or count == 0:
return True
return False
# Test cases
print(check_redundant_brackets("((a+b))")) # True
print(check_redundant_brackets("(a+(b*c))")) # False
C++
#include <iostream>
#include <string>
using namespace std;
bool checkRedundantBrackets(string expr) {
for (int i = 0; i < expr.length(); i++) {
if (expr[i] == ')') {
int j = i - 1;
bool hasOperator = false;
int count = 0;
while (j >= 0 && expr[j] != '(') {
if (expr[j] == '+' || expr[j] == '-' || expr[j] == '*' || expr[j] == '/') {
hasOperator = true;
}
count++;
j--;
}
if (!hasOperator || count == 0) {
return true;
}
}
}
return false;
}
int main() {
cout << boolalpha;
cout << checkRedundantBrackets("((a+b))") << endl; // true
cout << checkRedundantBrackets("(a+(b*c))") << endl; // false
return 0;
}
Java
public class RedundantBrackets {
public static boolean checkRedundantBrackets(String expr) {
for (int i = 0; i < expr.length(); i++) {
if (expr.charAt(i) == ')') {
int j = i - 1;
boolean hasOperator = false;
int count = 0;
while (j >= 0 && expr.charAt(j) != '(') {
char ch = expr.charAt(j);
if (ch == '+' || ch == '-' || ch == '*' || ch == '/') {
hasOperator = true;
}
count++;
j--;
}
if (!hasOperator || count == 0) {
return true;
}
}
}
return false;
}
public static void main(String[] args) {
System.out.println(checkRedundantBrackets("((a+b))")); // true
System.out.println(checkRedundantBrackets("(a+(b*c))")); // false
}
}
Optimized Approach
Explanation
A more efficient approach uses a stack data structure. The key insight is that when we encounter a closing bracket, we can check the characters between this bracket and its matching opening bracket.
The strategy works as follows:
- Push all opening brackets, operands, and operators onto the stack.
- When a closing bracket is found, start popping items until an opening bracket is found.
- If no operator is found between these brackets, then the brackets are redundant.
- If the stack becomes empty or we don't find any opening bracket, the expression is invalid.
Time Complexity: O(n) where n is the length of the expression
Space Complexity: O(n) for the stack
Consider the string “((a + b))”
Iterate from left to right.
i = 0 , we see an opening bracket so push it into the stack.
i = 1 , we see an opening bracket so push it into the stack.
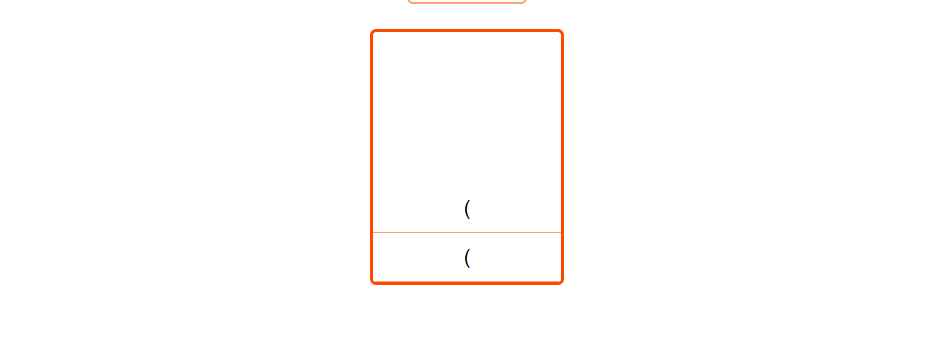
i = 2 , We read 'a' which is an operand. We don't push operands onto the stack, but process them directly.
i = 3 We read '+' which is an operator. We'll use it for calculation when we have both operands.
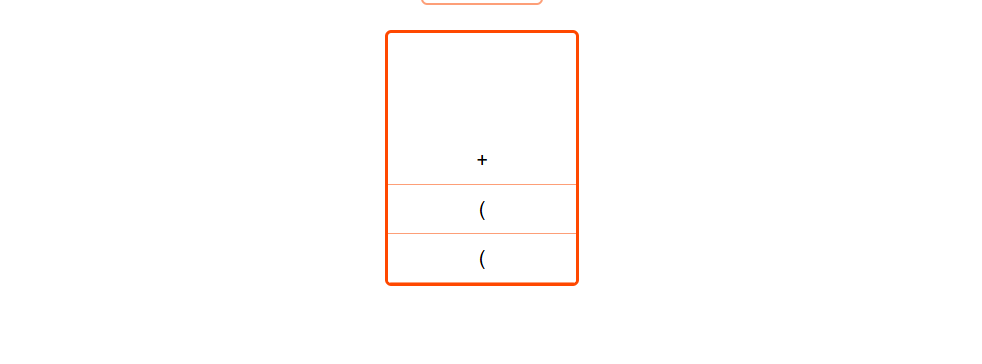
i = 4 We read 'b' which is an operand. We don't push operands onto the stack, but process them directly.
i = 5 we can see there is a closing bracket pop until we reach opening bracket.
i = 6 again a closing bracket , so pop from the stack.
We can see the stack is empty after processing all the characters so it is a valid sequence.
<visualization-box>
Code Implementation
Python
def check_redundant_brackets(expr):
stack = []
for char in expr:
# If current character is not a closing bracket, push to stack
if char != ')':
stack.append(char)
else:
# If immediate previous char is opening bracket, redundant brackets found
if stack[-1] == '(':
return True
# Pop until opening bracket is found
has_operator = False
while stack and stack[-1] != '(':
top = stack.pop()
if top in '+-*/':
has_operator = True
# Pop the opening bracket
if stack:
stack.pop()
if not has_operator:
return True
return False
# Test cases
print(check_redundant_brackets("((a+b))")) # True
print(check_redundant_brackets("(a+(b*c))")) # False
C++
#include <iostream>
#include <string>
#include <stack>
using namespace std;
bool checkRedundantBrackets(string expr) {
stack<char> s;
for (char ch : expr) {
if (ch != ')') {
s.push(ch);
} else {
if (s.top() == '(') {
return true;
}
bool hasOperator = false;
while (!s.empty() && s.top() != '(') {
char top = s.top();
if (top == '+' || top == '-' || top == '*' || top == '/') {
hasOperator = true;
}
s.pop();
}
if (!s.empty()) {
s.pop();
}
if (!hasOperator) {
return true;
}
}
}
return false;
}
int main() {
cout << boolalpha;
cout << checkRedundantBrackets("((a+b))") << endl; // true
cout << checkRedundantBrackets("(a+(b*c))") << endl; // false
return 0;
}
Java
import java.util.Stack;
public class RedundantBrackets {
public static boolean checkRedundantBrackets(String expr) {
Stack<Character> stack = new Stack<>();
for (int i = 0; i < expr.length(); i++) {
char ch = expr.charAt(i);
if (ch != ')') {
stack.push(ch);
} else {
if (stack.peek() == '(') {
return true;
}
boolean hasOperator = false;
while (!stack.isEmpty() && stack.peek() != '(') {
char top = stack.pop();
if (top == '+' || top == '-' || top == '*' || top == '/') {
hasOperator = true;
}
}
if (!stack.isEmpty()) {
stack.pop();
}
if (!hasOperator) {
return true;
}
}
}
return false;
}
public static void main(String[] args) {
System.out.println(checkRedundantBrackets("((a+b))")); // true
System.out.println(checkRedundantBrackets("(a+(b*c))")); // false
}
}
Conclusion
This problem shows how stacks can be effectively used to solve problems involving balanced parentheses and expression validation. The brute force approach works but is inefficient for large inputs, as it may require multiple passes through the same parts of the expression.
The optimized stack-based solution gives us a clean and efficient way to check for redundant brackets in a single pass through the expression, with clear time and space complexity advantages.
By learning both approaches, you can better appreciate the value of appropriate data structures in solving programming problems. Such pattern recognition can make many seemingly complex problems much more manageable.
