Check if Array is Sorted: Codes with Visualization
Raj Aryan is passionate about breaking down complex DSA concepts and making coding feel approachable for everyone. With over 500 problems solved on LeetCode, two hackathon wins under his belt, and a 3-star rating on CodeChef, he enjoys helping others level up their programming skills.
This seemingly simple operation forms the foundation for many algorithms and has practical applications in numerous programming scenarios.
Why does knowing if an array is sorted matter? First, many efficient algorithms (like binary search) only work on sorted data. Second, checking if data is already sorted can save unnecessary processing time - why sort what's already in order?
This article will explain how to check if an array is sorted, with clear examples and code implementations in various languages.
Understanding the Problem
What Makes an Array Sorted?
An array is considered sorted when its elements follow a specific order. The most common type of sorting is:
- Ascending order (also called increasing or non-decreasing): Each element is greater than or equal to the previous element.
For example, these arrays are sorted in ascending order:
- [1, 2, 3, 4, 5]
- [0, 0, 3, 7, 9]
- [-5, -3, 0, 4, 10]
These arrays are not sorted in ascending order:
- [5, 4, 3, 2, 1] (descending order)
- [1, 3, 2, 5, 4] (elements out of order)
An important detail is that consecutive equal elements are allowed in a sorted array. This is why we sometimes use the term "non-decreasing" rather than strictly "increasing" - the value can stay the same from one element to the next.
Special Cases
There are a few special cases to consider:
- An empty array is considered sorted (there's nothing out of order)
- An array with just one element is always sorted (there's no comparison needed)
- An array where all elements are equal is sorted (no element breaks the ordering)
Basic Approach
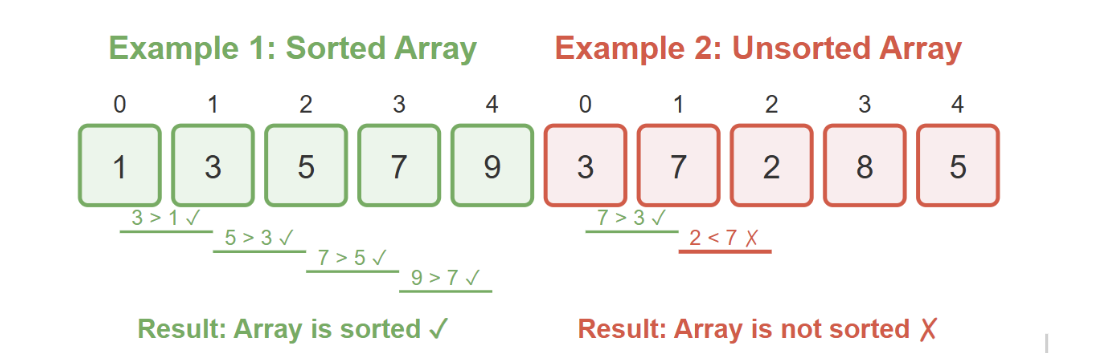
The most straightforward way to check if an array is sorted is to perform a linear traversal, comparing each element with its adjacent element.
Linear Traversal Method
- Start from the second element (index 1)
- Compare each element with the previous element
- If any element is less than its previous element, the array is not sorted
- If we reach the end without finding any such pair, the array is sorted
Time and Space Complexity
- Time Complexity: O(n), where n is the length of the array
- We need to check at most all elements once
- Best case: O(1) if we find elements out of order early
- Space Complexity: O(1)
- We only need a few variables regardless of input size
Check if Array is Sorted Visualization
<visualization-box>
Code Implementation
Let's look at how to implement this in several programming languages.
#include <iostream>
#include <vector>
bool isSorted(const std::vector<int>& arr) {
// Empty array or array with one element is always sorted
if (arr.size() <= 1) {
return true;
}
// Check each element with its previous element
for (int i = 1; i < arr.size(); i++) {
// If current element is less than previous, array is not sorted
if (arr[i] < arr[i-1]) {
return false;
}
}
// If we've checked all elements without returning false, array is sorted
return true;
}
int main() {
std::vector<int> sortedArray = {1, 2, 3, 4, 5};
std::vector<int> unsortedArray = {5, 2, 7, 1, 9};
std::cout << "Is sortedArray sorted? " << (isSorted(sortedArray) ? "Yes" : "No") << std::endl;
std::cout << "Is unsortedArray sorted? " << (isSorted(unsortedArray) ? "Yes" : "No") << std::endl;
return 0;
}
Python Implementation
def is_sorted(arr):
# Empty array or array with one element is always sorted
if len(arr) <= 1:
return True
# Check each element with its previous element
for i in range(1, len(arr)):
# If current element is less than previous, array is not sorted
if arr[i] < arr[i-1]:
return False
# If we've checked all elements without returning false, array is sorted
return True
# Test cases
sorted_array = [1, 2, 3, 4, 5]
unsorted_array = [5, 2, 7, 1, 9]
print(f"Is sorted_array sorted? {'Yes' if is_sorted(sorted_array) else 'No'}")
print(f"Is unsorted_array sorted? {'Yes' if is_sorted(unsorted_array) else 'No'}")
Java Implementation
public class ArraySortCheck {
public static boolean isSorted(int[] arr) {
// Empty array or array with one element is always sorted
if (arr.length <= 1) {
return true;
}
// Check each element with its previous element
for (int i = 1; i < arr.length; i++) {
// If current element is less than previous, array is not sorted
if (arr[i] < arr[i-1]) {
return false;
}
}
// If we've checked all elements without returning false, array is sorted
return true;
}
public static void main(String[] args) {
int[] sortedArray = {1, 2, 3, 4, 5};
int[] unsortedArray = {5, 2, 7, 1, 9};
System.out.println("Is sortedArray sorted? " + (isSorted(sortedArray) ? "Yes" : "No"));
System.out.println("Is unsortedArray sorted? " + (isSorted(unsortedArray) ? "Yes" : "No"));
}
}
Algorithm Explanation
Let's walk through how the algorithm works with a visual example.
Consider the array [3, 6, 8, 10, 9, 15]:
- Start at index 1 (value 6)
- Compare with previous element (index 0, value 3)
- 6 > 3, so continue
- Move to index 2 (value 8)
- Compare with previous element (index 1, value 6)
- 8 > 6, so continue
- Move to index 3 (value 10)
- Compare with previous element (index 2, value 8)
- 10 > 8, so continue
- Move to index 4 (value 9)
- Compare with previous element (index 3, value 10)
- 9 < 10, so return false
The algorithm detected that 9 is less than 10, breaking the ascending order. It correctly returns false without checking the rest of the array.
Edge Cases
Let's examine how our algorithm handles special cases:
Empty Arrays
For an empty array [], the check if (arr.length <= 1) returns true immediately. This makes sense because an empty array has no elements that could be out of order.
Arrays With One Element
Similarly, an array with a single element like [5] is also sorted by definition, and our algorithm correctly returns true.
Arrays With Duplicate Elements
The algorithm handles duplicate elements correctly:
- [1, 2, 2, 3, 4] is sorted because each element is greater than or equal to the previous one
- [1, 2, 2, 1, 4] is not sorted because 1 < 2
Variations of the Problem
Checking for Decreasing Order
To check if an array is sorted in decreasing order, we simply need to modify our comparison:
def is_sorted_decreasing(arr):
if len(arr) <= 1:
return True
for i in range(1, len(arr)):
# Check if current element is greater than previous
if arr[i] > arr[i-1]:
return false
return True
Checking if Array is Sorted and Rotated
A more complex variation is determining if an array was once sorted but has been rotated. For example, [3, 4, 5, 1, 2] is a sorted array [1, 2, 3, 4, 5] that was rotated to the right by 3 positions.
To solve this, we need to:
- Find the number of "drops" where arr[i] < arr[i-1]
- If there's exactly one drop and the first element is ≥ the last element, the array is sorted and rotated
def is_sorted_and_rotated(arr):
if len(arr) <= 1:
return True
drops = 0
n = len(arr)
for i in range(1, n):
if arr[i] < arr[i-1]:
drops += 1
# Check the wrap-around case (last and first element)
if arr[0] < arr[n-1]:
drops += 1
# A sorted and rotated array has exactly one drop
return drops <= 1
Optimization Techniques
Early Termination
One advantage of our approach is early termination. As soon as we find elements out of order, we return false. This means for unsorted arrays, we often don't need to check all elements.
For example, in array [1, 5, 3, 8, 9], we only need to check up to index 2 to determine it's not sorted.
Performance Considerations
For very large arrays, the linear approach is still the best general solution. However, in certain contexts, we can make optimizations:
- If the array is frequently modified and we need to check if it's sorted often, consider maintaining a "sorted" flag that gets updated with each modification.
- For parallelized systems dealing with massive arrays, you could split the array checking among multiple processors, though this introduces overhead and might not be worth it for this simple operation.
Applications
Checking if an array is sorted has several practical applications:
- Optimization in Sorting Algorithms: Many sorting implementations first check if the array is already sorted to avoid unnecessary work.
- Prerequisite for Binary Search: Before performing a binary search, it's crucial to ensure the array is sorted.
- Data Integrity Validation: In systems where data should maintain a specific order, this check serves as a validation step.
- Adaptive Algorithms: Some algorithms behave differently based on whether input data is sorted.
Conclusion
Checking if an array is sorted is a fundamental operation in programming. While the solution might seem obvious—compare each element with its predecessor, understanding the disturbance helps build a stronger foundation for more complex algorithms.
The linear traversal method offers an efficient O(n) time complexity solution with constant space requirements. This approach works across different programming languages and handles all edge cases properly.
As you progress in your programming journey, you'll find that this simple check appears in many contexts, from optimizing algorithms to validating data integrity. By mastering this basic operation, you're building important skills for tackling more complex array manipulations and sorting algorithms.
