Kth Largest Sum Subarray: Codes with Visualization
Raj Aryan is passionate about breaking down complex DSA concepts and making coding feel approachable for everyone. With over 500 problems solved on LeetCode, two hackathon wins under his belt, and a 3-star rating on CodeChef, he enjoys helping others level up their programming skills.
It tests your ability to work with arrays and optimization techniques. Let's explore how to solve it step by step!
Problem Statement
Given an array of integers and a number k, we need to find the kth largest sum among all possible contiguous subarrays.
For example, if we have an array [1, 2, 3, 4] and k = 2, the sums of all possible subarrays are:
- [1] = 1
- [2] = 2
- [3] = 3
- [4] = 4
- [1,2] = 3
- [2,3] = 5
- [3,4] = 7
- [1,2,3] = 6
- [2,3,4] = 9
- [1,2,3,4] = 10
Sorting these sums: [1, 2, 3, 3, 4, 5, 6, 7, 9, 10]
The 2nd largest sum is 9.
Brute Force Approach
Explanation
The simplest way to solve this problem is to:
- Generate all possible subarrays
- Calculate the sum of each subarray
- Store all sums in an array
- Sort the array of sums
- Return the kth largest element
For an array of size n, there are n(n+1)/2 possible subarrays, so we'll need to calculate that many sums.
The time complexity of this approach is O(n² log(n²)), where n² comes from generating all subarrays and log(n²) from sorting them.
Step 1 : Generate all Subarrays
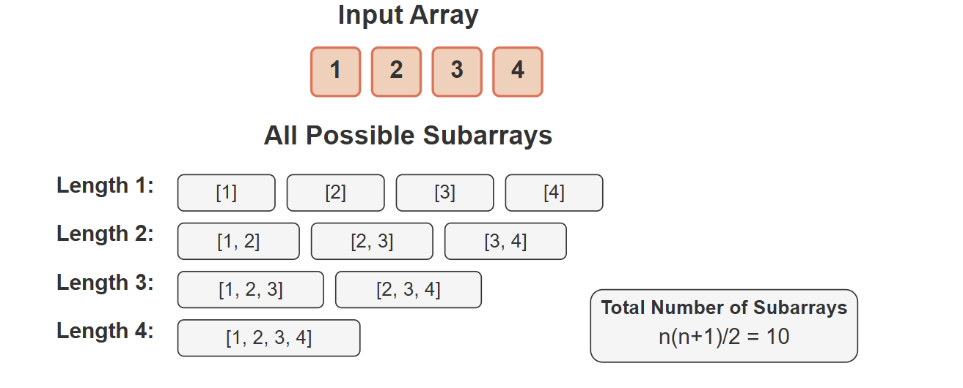
Step 2 : Calculate sum of each subarray
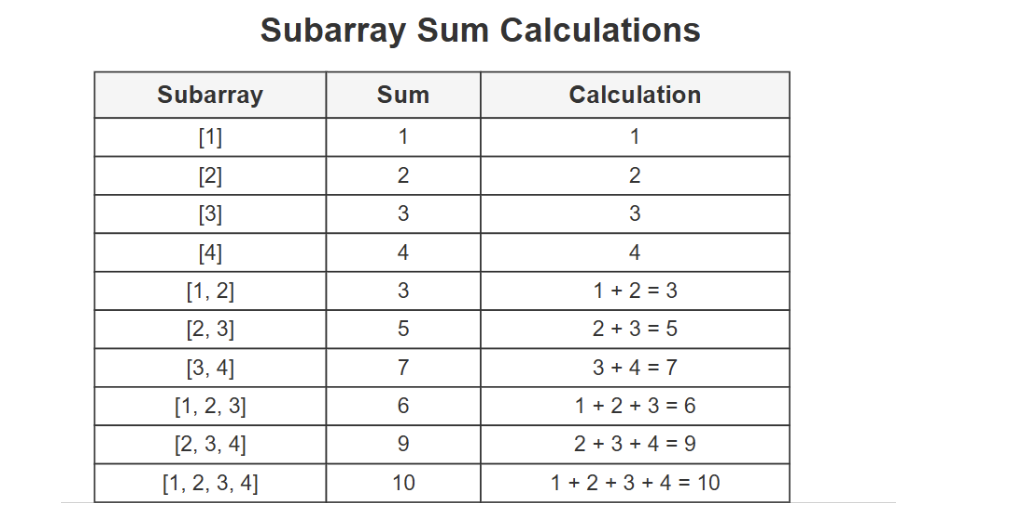
Step 3-5 : Sorts sums and find kth largest
Code (Python)
def kth_largest_subarray_sum_brute(arr, k):
n = len(arr)
sums = []
# Generate all possible subarrays and their sums
for i in range(n):
current_sum = 0
for j in range(i, n):
current_sum += arr[j]
sums.append(current_sum)
# Sort sums in descending order
sums.sort(reverse=True)
# Return the kth largest sum
return sums[k-1]
# Example
arr = [1, 2, 3, 4]
k = 2
print(kth_largest_subarray_sum_brute(arr, k)) # Output: 9Code (C++)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int kthLargestSubarraySum(vector<int>& arr, int k) {
int n = arr.size();
vector<int> sums;
// Generate all possible subarrays and their sums
for (int i = 0; i < n; i++) {
int current_sum = 0;
for (int j = i; j < n; j++) {
current_sum += arr[j];
sums.push_back(current_sum);
}
}
// Sort sums in descending order
sort(sums.begin(), sums.end(), greater<int>());
// Return the kth largest sum
return sums[k-1];
}
int main() {
vector<int> arr = {1, 2, 3, 4};
int k = 2;
cout << kthLargestSubarraySum(arr, k) << endl; // Output: 9
return 0;
}Code (Java)
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class KthLargestSubarraySum {
public static int kthLargestSubarraySum(int[] arr, int k) {
int n = arr.length;
List<Integer> sums = new ArrayList<>();
// Generate all possible subarrays and their sums
for (int i = 0; i < n; i++) {
int currentSum = 0;
for (int j = i; j < n; j++) {
currentSum += arr[j];
sums.add(currentSum);
}
}
// Sort sums in descending order
Collections.sort(sums, Collections.reverseOrder());
// Return the kth largest sum
return sums.get(k-1);
}
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4};
int k = 2;
System.out.println(kthLargestSubarraySum(arr, k)); // Output: 9
}
}Optimized Approach
Explanation
While the brute force approach works for small arrays, it can be too slow for larger ones. We can optimize by:
- Using a min-heap (priority queue) to keep track of the k largest sums
- For each subarray sum, if the heap size is less than k, add the sum to the heap
- If the heap size is k and the current sum is greater than the smallest element in the heap, remove the smallest element and add the current sum
- After processing all subarrays, the smallest element in the heap will be our kth largest sum
This approach still requires generating all possible subarrays but avoids sorting the entire list of sums.
The time complexity is O(n² log k), which is better than O(n² log(n²)) when k is much smaller than n².
Kth Missing Positive Number Visualization
<visualization-box>
Code (Python)
import heapq
def kth_largest_subarray_sum_optimized(arr, k):
n = len(arr)
min_heap = []
# Generate all possible subarrays and their sums
for i in range(n):
current_sum = 0
for j in range(i, n):
current_sum += arr[j]
# If heap size is less than k, add sum
if len(min_heap) < k:
heapq.heappush(min_heap, current_sum)
# If current sum is greater than smallest in heap, replace it
elif current_sum > min_heap[0]:
heapq.heappop(min_heap)
heapq.heappush(min_heap, current_sum)
# Return smallest element in heap (kth largest overall)
return min_heap[0]
# Example
arr = [1, 2, 3, 4]
k = 2
print(kth_largest_subarray_sum_optimized(arr, k)) # Output: 9Code (C++)
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int kthLargestSubarraySumOptimized(vector<int>& arr, int k) {
int n = arr.size();
priority_queue<int, vector<int>, greater<int>> min_heap;
// Generate all possible subarrays and their sums
for (int i = 0; i < n; i++) {
int current_sum = 0;
for (int j = i; j < n; j++) {
current_sum += arr[j];
// If heap size is less than k, add sum
if (min_heap.size() < k) {
min_heap.push(current_sum);
}
// If current sum is greater than smallest in heap, replace it
else if (current_sum > min_heap.top()) {
min_heap.pop();
min_heap.push(current_sum);
}
}
}
// Return smallest element in heap (kth largest overall)
return min_heap.top();
}
int main() {
vector<int> arr = {1, 2, 3, 4};
int k = 2;
cout << kthLargestSubarraySumOptimized(arr, k) << endl; // Output: 9
return 0;
}Code (Java)
import java.util.PriorityQueue;
public class KthLargestSubarraySumOptimized {
public static int kthLargestSubarraySumOptimized(int[] arr, int k) {
int n = arr.length;
// Min heap to keep the k largest sums
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
// Generate all possible subarrays and their sums
for (int i = 0; i < n; i++) {
int currentSum = 0;
for (int j = i; j < n; j++) {
currentSum += arr[j];
// If heap size is less than k, add sum
if (minHeap.size() < k) {
minHeap.add(currentSum);
}
// If current sum is greater than smallest in heap, replace it
else if (currentSum > minHeap.peek()) {
minHeap.poll();
minHeap.add(currentSum);
}
}
}
// Return smallest element in heap (kth largest overall)
return minHeap.peek();
}
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4};
int k = 2;
System.out.println(kthLargestSubarraySumOptimized(arr, k)); // Output: 9
}
}Conclusion
We tackled the "Kth Largest Sum Subarray" problem using two approaches:
1.Brute Force: Simple but less efficient at O(n² log(n²)) time complexity
2.Optimized Approach: Better performance at O(n² log k) time complexity using a min-heap
The optimized solution significantly improves efficiency when k is much smaller than n², which is often the case in practice. This kind of optimization shows how data structures like heaps can improve algorithm performance.
This problem helps build skills in array manipulation, subarray processing, and priority queue usage—fundamental techniques that apply to many other programming challenges.
