Rotate Array by K Elements: Codes with Visualization
Raj Aryan is passionate about breaking down complex DSA concepts and making coding feel approachable for everyone. With over 500 problems solved on LeetCode, two hackathon wins under his belt, and a 3-star rating on CodeChef, he enjoys helping others level up their programming skills.
Problem Statement
Given an array of integers and an integer k, rotate the array to the right by k positions.
For example:
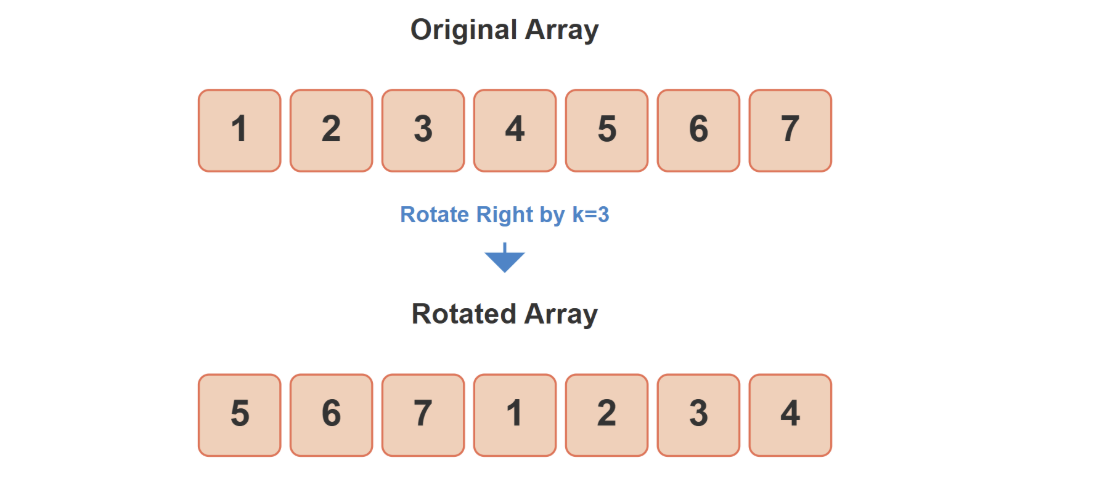
- Input: [1, 2, 3, 4, 5, 6, 7], k = 3
- Output: [5, 6, 7, 1, 2, 3, 4]
This means the last k elements move to the front, while the rest shift to the right.
Brute Force Approach
Explanation
The simplest way to approach this problem is to perform k single-step rotations. In each rotation, we move the last element to the first position and shift all other elements one step to the right.
This method is intuitive but not very efficient, especially for large arrays or large values of k.
Time Complexity: O(n×k) - where n is the array length and k is the number of rotations
Space Complexity: O(1) - we use a constant amount of extra space
Code (Python)
def rotate_array_brute_force(nums, k):
n = len(nums)
# Handle case where k > n
k = k % n
# Perform k single rotations
for _ in range(k):
# Store the last element
last = nums[n-1]
# Shift all elements one position to the right
for i in range(n-1, 0, -1):
nums[i] = nums[i-1]
# Place the last element at the beginning
nums[0] = last
return nums
# Example usage
arr = [1, 2, 3, 4, 5, 6, 7]
k = 3
print(rotate_array_brute_force(arr, k)) # Output: [5, 6, 7, 1, 2, 3, 4]
Code (C++)
#include <vector>
std::vector<int> rotateArrayBruteForce(std::vector<int>& nums, int k) {
int n = nums.size();
// Handle case where k > n
k = k % n;
// Perform k single rotations
for (int j = 0; j < k; j++) {
// Store the last element
int last = nums[n-1];
// Shift all elements one position to the right
for (int i = n-1; i > 0; i--) {
nums[i] = nums[i-1];
}
// Place the last element at the beginning
nums[0] = last;
}
return nums;
}
// Example usage
// int main() {
// std::vector<int> arr = {1, 2, 3, 4, 5, 6, 7};
// int k = 3;
// rotateArrayBruteForce(arr, k);
// // Output: [5, 6, 7, 1, 2, 3, 4]
// return 0;
// }
Code (Java)
import java.util.Arrays;
public class ArrayRotation {
public static int[] rotateArrayBruteForce(int[] nums, int k) {
int n = nums.length;
// Handle case where k > n
k = k % n;
// Perform k single rotations
for (int j = 0; j < k; j++) {
// Store the last element
int last = nums[n-1];
// Shift all elements one position to the right
for (int i = n-1; i > 0; i--) {
nums[i] = nums[i-1];
}
// Place the last element at the beginning
nums[0] = last;
}
return nums;
}
// Example usage
// public static void main(String[] args) {
// int[] arr = {1, 2, 3, 4, 5, 6, 7};
// int k = 3;
// rotateArrayBruteForce(arr, k);
// // Output: [5, 6, 7, 1, 2, 3, 4]
// }
}Optimized Approach
Explanation
The optimized solution uses the reversal algorithm, which is much more efficient:
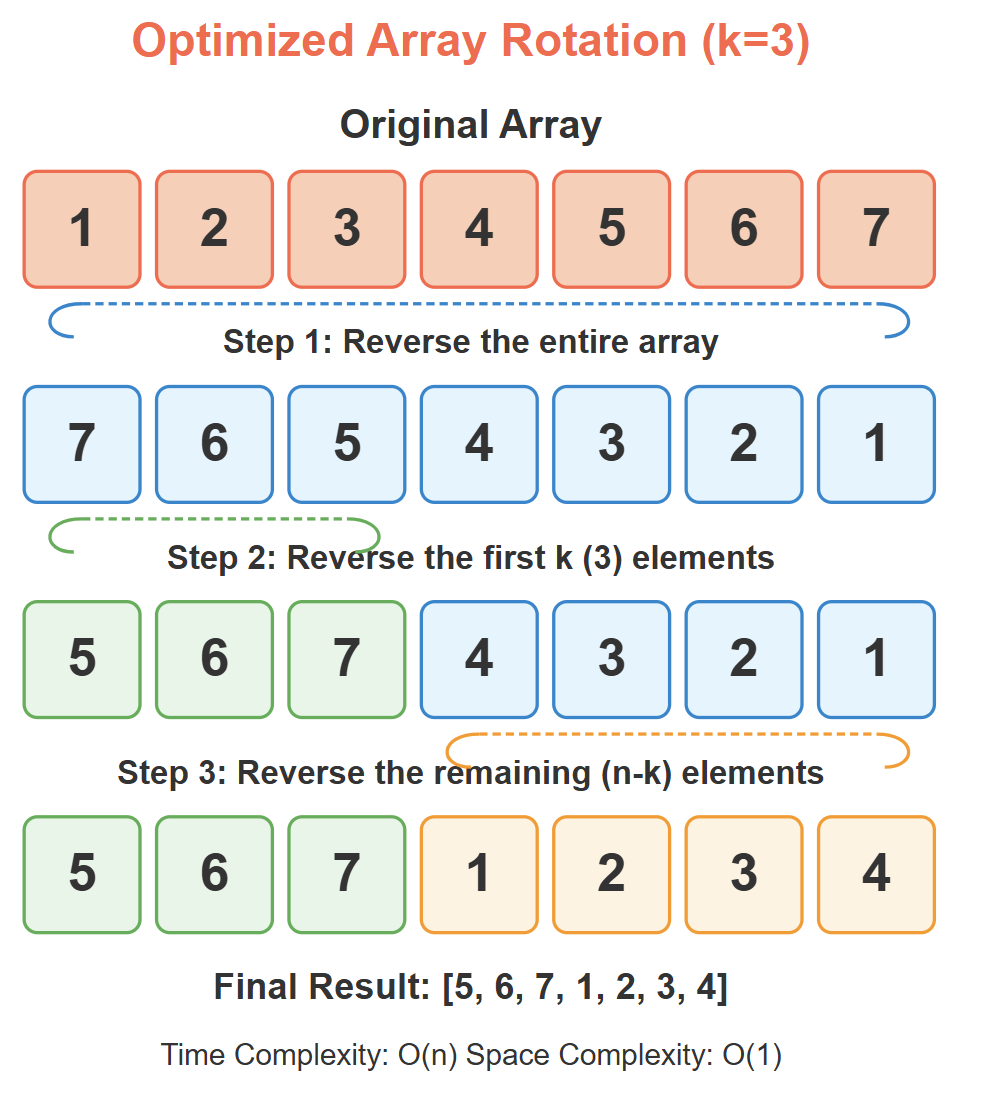
- Reverse the entire array.
- Reverse the first k elements.
- Reverse the remaining n-k elements.
This approach works because:
- When we reverse the entire array, the elements that should be at the front end up at the back, but in reverse order.
- Reversing the first k elements puts them in the correct order.
- Reversing the remaining elements also puts them in the correct order.
Let's trace through an example:
- Original array: [1, 2, 3, 4, 5, 6, 7], k = 3
- After reversing entire array: [7, 6, 5, 4, 3, 2, 1]
- After reversing first k elements: [5, 6, 7, 4, 3, 2, 1]
- After reversing remaining elements: [5, 6, 7, 1, 2, 3, 4]
Time Complexity: O(n) - we only need to traverse the array a fixed number of times
Space Complexity: O(1) - we use a constant amount of extra space
Array Rotation Algorithm Visualization
<visualization-box>
Code (Python)
def rotate_array_optimized(nums, k):
n = len(nums)
# Handle case where k > n
k = k % n
# Helper function to reverse a portion of the array
def reverse(start, end):
while start < end:
nums[start], nums[end] = nums[end], nums[start]
start += 1
end -= 1
# Step 1: Reverse the entire array
reverse(0, n-1)
# Step 2: Reverse the first k elements
reverse(0, k-1)
# Step 3: Reverse the remaining n-k elements
reverse(k, n-1)
return nums
# Example usage
arr = [1, 2, 3, 4, 5, 6, 7]
k = 3
print(rotate_array_optimized(arr, k)) # Output: [5, 6, 7, 1, 2, 3, 4]
Code (C++)
#include <iostream>
#include <vector>
#include <algorithm>
std::vector<int> rotateArrayOptimized(std::vector<int>& nums, int k) {
int n = nums.size();
// Handle case where k > n
k = k % n;
// Step 1: Reverse the entire array
std::reverse(nums.begin(), nums.end());
// Step 2: Reverse the first k elements
std::reverse(nums.begin(), nums.begin() + k);
// Step 3: Reverse the remaining n-k elements
std::reverse(nums.begin() + k, nums.end());
return nums;
}
// We can also implement our own reverse function instead of using std::reverse
void reverse(std::vector<int>& nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
// Example usage
// int main() {
// std::vector<int> arr = {1, 2, 3, 4, 5, 6, 7};
// int k = 3;
// rotateArrayOptimized(arr, k);
// // Output: [5, 6, 7, 1, 2, 3, 4]
// return 0;
// }
Code (Java)
import java.util.Arrays;
public class ArrayRotation {
public static int[] rotateArrayOptimized(int[] nums, int k) {
int n = nums.length;
// Handle case where k > n
k = k % n;
// Step 1: Reverse the entire array
reverse(nums, 0, n-1);
// Step 2: Reverse the first k elements
reverse(nums, 0, k-1);
// Step 3: Reverse the remaining n-k elements
reverse(nums, k, n-1);
return nums;
}
// Helper function to reverse a portion of the array
private static void reverse(int[] nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
// Example usage
// public static void main(String[] args) {
// int[] arr = {1, 2, 3, 4, 5, 6, 7};
// int k = 3;
// rotateArrayOptimized(arr, k);
// // Output: [5, 6, 7, 1, 2, 3, 4]
// }
}
Conclusion
We've explored two different approaches to rotate an array:
1. The brute force approach which is simple to implement but inefficient with O(n×k) time complexity.
2. The optimized reversal algorithm which achieves O(n) time complexity.
The reversal algorithm is an excellent example of how a seemingly complex problem can be solved with a clever trick. By breaking down the rotation into three simple reversal operations, we can achieve a much more efficient solution.
This problem teaches an important lesson about algorithmic thinking - looking beyond the obvious approach can lead to significant performance improvements. The ability to transform a problem or view it from a different angle is a valuable skill in programming.
